1.2. Systems and Models¶
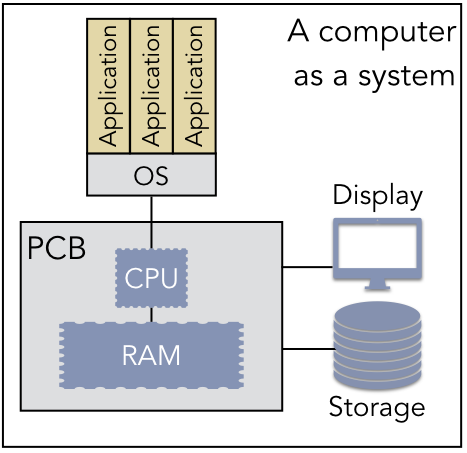
Throughout this book, we are considering the idea of computer systems from a perspective that strives to apply insights from systems theory. From this view, a system is an integrated collection of entities and their interactions. The computer itself is a system. Computers are assembled from disparate hardware components that include a central processing unit (CPU), storage devices, input and output devices, random access memory (RAM) cards, and a printed circuit board (PCB) that links them all together. A software OS executes on top of these components, thus integrating their independent functionality into a more complex entity. To fully understand the nature of the computer as a whole, it’s important to understand the components’ independent functionality as well as how they work together.
The system is made more complex by adding application software to the mix. Each application is constructed from code modules, variables, and other run-time memory structures that are compiled and integrated to provide a single higher-level function. But software does not run itself; the software must be executed within the greater context of computing, as a sequence of steps performed by a physical computer with the help of an OS. Some applications run in isolation from one another, but they still require the OS and hardware. Others communicate with services that provide information or perform complimentary tasks, allowing the developer to build more powerful software without having to start from scratch. Figure 1.2.1 summarizes this view of the computer as a system of interacting components.
In short, all of computing is a system. As computer scientists continue to explore the power of computing, we can take this claim even further to suggest that computing is made up of a system of systems. In order to stream a movie over the Internet, the application software must integrate network connectivity and local file storage, probably with the help of a graphics processing unit (GPU) that improves the visual quality of the experience. Each of these hardware and software components are systems, and the application is coordinating their interaction to serve the user. As another example, consider large-scale scientific projects that model changes in the climate or advanced quantum mechanics phenomena. This type of work involves linking thousands of parallel computing nodes that coordinate their calculations and exchange data as needed, creating truly complicated systems and interactions. Our goal is to understand the common principles and strategies that make these systems work.
1.2.1. Models as Representations¶
A first step toward understanding a system is constructing a model – a simplified representation – of the system. Figure 1.2.1 above is a model of a computer as a system. As a simplification, models necessarily omit details that are present in the system itself. Some models have visual representations, facilitating human interpretation of the system. That is, visual models are very good tools for people to make sense of the entities and their interactions. System designers, developers, and users can use visual models to avoid mistakes. Other models are formal, written in a mathematical specification language. One way to characterize the differences between models is to describe their level of abstraction. Visual models may have a relatively low level of abstraction, including details that are aesthetically pleasing but not important. Formal models have a relatively high level of abstraction, omitting everything except the bare minimum.
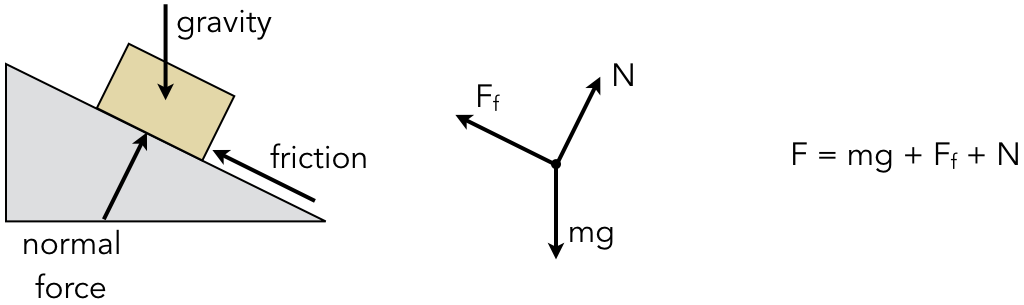
Consider the models shown in Figure 1.2.2. The model on the left has the lowest level of abstraction, as it includes details that show a yellow box on a grey ramp. This scenario is then converted into a free-body diagram in the middle. Free-body diagrams are used in physics to illustrate the forces acting on an object, while removing unneeded details such as the drawing of the box and the ramp. The equation on the right is the formal model that captures this information. The net force F is the sum of the forces created by gravity (mg), the normal force N, and the force of friction \(F_f\). All three models convey the same information, but they provide different levels of abstraction.
A static (or structural) model describes the fixed, unchanging features of a system, while omitting explanations of how the system or entities change. Readers with a background in object-oriented programming may be familiar with class diagrams created using unified modeling language (UML). These models describe features like class inheritance and sub-typing, while omitting characteristics like the values of an object’s variables or the messages it uses to communicate with other objects. Throughout this text, we will focus repeatedly on one particular type of static model, the system architecture.
In contrast, a dynamic (or behavioral) model focuses on changes to the system. These models are particularly important to understanding systems, because many of their key features are emergent properties. An emergent property is one that results from the dynamic features of the system and is not intuitive from static models alone. We will be using two dynamic UML models throughout this book. A state model describes the system’s possible states – defined by meaningful combinations of system parameters – and the possible transitions between them. For instance, a streaming video service may characterize different states to represent “requesting the video,” “buffering received data,” “pausing the video,” and “playing the video.” A sequence model illustrates the order of messages and key events that a system experiences over time. One use of a sequence model is to describe a specific order in which state transitions occur. These models provide a clear illustration of network communication protocols and messages to coordinate parallel and distributed computation.
1.2.2. From Models to Implementations¶
Models are useful tools for analyzing and illustrating the behavior of a system. Well-constructed models of the natural world can help scientists develop insight into and explain real-world phenomena, such as the chemical reactions that release energy stored in food, the wave-like behavior of electrons in an atom, or the fractal designs in crystals. User manuals for appliances, vehicles, children’s toys, etc., use illustrations as models to convey information to consumers who are not necessarily experts in the field.
In contrast to many other fields, the field of computer systems places a strong emphasis on turning models into implementations. That is, our goal is not simply to build and interpret models, but to turn these models into working artifacts. This implementation process can be quite challenging and creates many opportunities for errors; mistakes that cause the system to behave differently from the model can render the model useless or, even worse, increase confusion. As such, much of our focus throughout this book is on successfully turning models into concrete, executable implementations.