9.5. Timing in Distributed Environments¶

9.5.1. Clock Synchronization¶

Figure 9.5.1: Sequence of messages and events in NTP

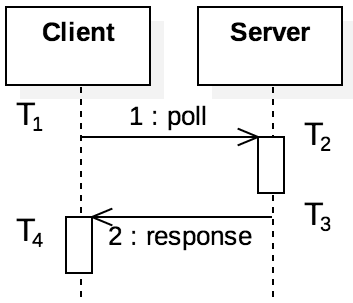
One approach to solving the timing problem in distributed environments is to synchronize the clocks on all nodes with a centralized server. Figure 9.5.1 shows the exchange of messages in the Network Time Protocol (NTP), one solution built on this idea. In NTP, each node will occasionally poll the server, keeping track of the times when certain events occur. Specifically, the client records $T_1$ as the time that it sent the poll message. The server received the message at $T_2$ according to its internal clock, sending the response back at time $T_3$ (according to the server’s clock). The client then records $T_4$ as the time that it received the response from the server. Based on this information, the client would calculate two values:

The delay is used to eliminate the time that it takes for the messages to travel through the network from consideration. The offset is used to detect the clock skew between the nodes. For instance, assume $T_1 = 20$, $T_2 = 30$, $T_3 = 32$, and $T_4 = 46$. Then the offset would be calculated as $(10 - 14)/2 = -2$, and the delay would be $26 - 2 = 24$. The message from client to server was measured as taking 10 time units, whereas the response took longer (14 time units). One possible cause is that the client’s clock is ahead of the server’s clock. If the client’s clock was adjusted back so that $T_1 = 18$ and $T_4 = 44$, then the offset would be 0, as the two messages would be measured as taking 12 time units in each direction. The client passes the offset and delay values, along with previous measurements, through a suite of protocols to filter and select the most accurate values. The client then combines these survivor offsets to adjust the system clock time and frequency. The protocol can then be repeated until the offset is sufficiently small. [1]

9.5.2. Logical Clocks and Lamport Timestamps¶

As systems grow larger and nodes increase in physical distance, trying to synchronize the internal clocks of nodes in the system becomes unmanageable. The number of messages needed for protocols like NTP impose a significant burden on the network that would interfere with other work. An alternative approach is to establish a reasonable understanding of the sequence of events using logical clocks. A logical clock uses messages, not real time measurements, to track the relative, logical ordering of events. These messages are asynchronous, in the sense that there are no timing guarantees; network and other processing delays introduce random timing differences between when a message is sent and received.

Lamport timestamps are a simple approach to logical clocks. Each process (a task running on a separate node) maintains an internal counter of events that it experiences. These events could be a local action or computational result that is relevant to the system as a whole. Whenever a local event occurs, or a process sends or receives a message, this internal counter is incremented. When processes send messages, they append their counter. Given their distributed nature, processes can only observe local events and messages they send or receive; they cannot be aware of messages received by other processes or events that occur elsewhere in the system. Code Listing 9.9 shows the basic algorithm for receiving a message with a Lamport timestamp. The message’s timestamp is compared with the local process’s counter, and the local timestamp is updated to be the greater of the two. The timestamp is then incremented, keeping track of the event of receiving the message.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

/* Code Listing 9.9:
   Reading a message from a socket with a Lamport timestamp attached
 */

ssize_t bytes = read (socketfd, &message, sizeof (message));
/* Update local timestamp if message has greater value */
if (message.timestamp > local_timestamp)
  local_timestamp = message.timestamp;
/* Increment local timestamp */
local_timestamp++;

Figure 9.5.2: Events and messages using logical clocks

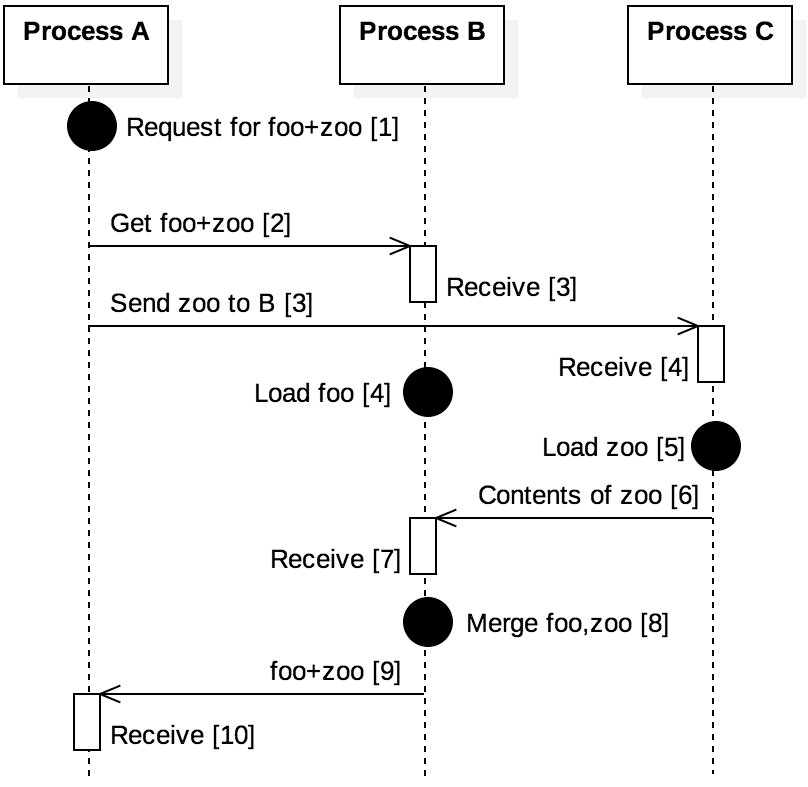
As an example, consider a cloud computing system that provides Internet-accessible data storage service. Figure 9.5.2 shows a sample sequence of events that may occur; the numbers in brackets denote the Lamport timestamps. Process A provides an interface for users and receives a request for the files “foo” and “zoo”; this request constitutes a local event for A, which has the timestamp 1. A then sends a message to process B (timestamp 2) and another to process C (timestamp 3); receiving these messages occur at times 3 and 4, respectively. Note that process B has no knowledge of the message sent to C, so B’s local timestamp only reflects its knowledge of the message it received.

After receiving their messages from process A, processes B and C concurrently load the two files requested. C sends the contents of “zoo” to B (timestamp 6) and B receives this message. Note that B’s timestamp jumps from 4 to 7 when this happens, reflecting the timestamp it observes in the message from C. B then merges the files (timestamp 8) and sends the result to A.

With logical clocks, it is critical to note that an earlier timestamp does not necessarily guarantee that an event occurred before one with a later timestamp. Consider process B’s perspective in Figure 9.5.2. B observes the local logical ordering of events at timestamps 3, 4, and 7. However, B cannot know if “foo” was loaded before or after “zoo.” In fact, B cannot even know that the message it received from A was sent before the message from A to C. B can only observe the logical ordering of events within its own time line. If B later receives a message from A with a timestamp greater than 11, it knows that message comes after the message when it sent foo+zoo to A. However, if B’s next interaction with C is receiving a message with timestamp 11, B cannot determine precisely when this message was sent; it’s possible that C experienced several events before B merged the files at timestamp 8.

In summary, logical clocks provide a mechanism for processes to exchange information about the relative ordering of events based on their perspectives. If processes A and B exchange messages back and forth, they can determine the relative ordering of these events. Once a third process C starts exchanging messages with A, process A will be able to determine the relative ordering of these messages, but neither B nor C would have the full view of the exchanges.

9.5.3. Vector Clocks¶

Figure 9.5.2 illustrates one of the shortcomings of logical clocks with Lamport timestamps. Note that process A’s timeline jumps from timestamp 3 to the message it receives from B with timestamp 9. Given only this information, process A could not distinguish this sequence of events from a different timeline in which B experienced only local events. That is, the timestamp that process A observes in the message from B does not even provide assurance that B received the original message from A, nor does it suggest that B has been communicating with C. Lamport timestamps alone do not provide sufficient information to distinguish these scenarios.

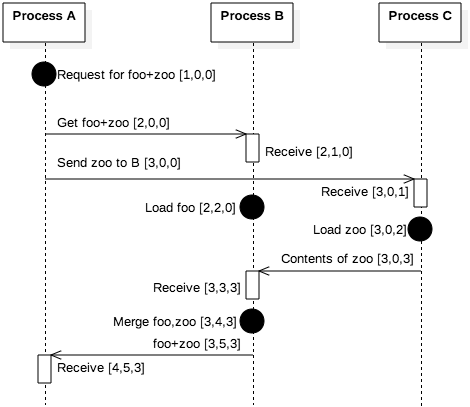
Figure 9.5.3: The events of Figure 9.5.2 with vector clocks

Vector clocks extend the basic idea of logical clocks with more information to address this problem. Whereas logical clocks kept only a single counter to establish the relative ordering of events, vector clocks use one counter per process. When a process sends a message, it appends the vector of counters from its perspective, implicitly acknowledging its understanding of the other process’s timestamps. Figure 9.5.3 illustrates the same sequence of events from Figure 9.5.2, using vector clocks instead of Lamport timestamps. When process B receives the first message from A, B increments its own counter in the vector.

Figure 9.5.3 illustrates a key strength of vector clocks with the message from process C to B containing the contents of zoo. This message contains the vector [3,0,3], indicating that C believes process A’s timestamp is at least 3. But B had previously received the vector [2,0,0] from process A, so process B knows that A’s message to C was sent after A’s message to B. Note, though, that process B cannot be certain about the order of events that C experienced. That is, the vector [2,0,0] was A stating it believed C’s timestamp was 0. The best that process B can state is that the message it received from C had been sent after A sent the first message to B. For an asynchronous system, this claim is the best that can be made.