8.5. Dining Philosophers Problem and Deadlock¶

The previous chapter introduced the concept of deadlock. Deadlock is the permanent blocking of two or more threads based on four necessary conditions. The first three are general properties of synchronization primitives that are typically unavoidable. The last is a system state that arises through a sequence of events.

• Mutual exclusion: Once a resource has been acquired up to its allowable capacity, no other thread is granted access.
• No preemption: Once a thread has acquired a resource, the resource cannot be forcibly taken away. For instance, only the owner of a mutex can unlock it.
• Hold and wait: It is possible that a thread can acquire one resource and retain ownership of that resource while waiting on another.
• Circular wait: One thread needs a resource held by another, while this second thread needs a different resource held by the first.

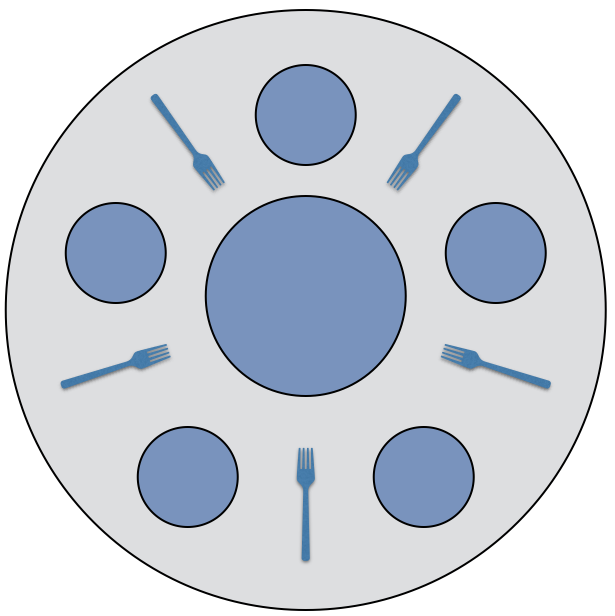
Figure 8.5.1: Providing the same number of plates and forks creates a problem for a set of dining philosophers

The dining philosophers problem is a metaphor that illustrates the problem of deadlock. The scenario consists of a group of philosophers sharing a meal at a round table. As philosophers, they like to take some time to think; but they are at a meal, so they also need to eat. As illustrated in Figure 8., there is a large serving dish in the middle of the table. Every philosopher has a plate and two serving forks, one to their right and one to their left. When a philosopher decides that they are hungry enough, they stop thinking and grab the forks to serve themselves from the serving dish in the middle.

The problem arises when all of the philosophers decide to eat at the same time. Consider the case where all of the philosophers independently decide that they will try to grab the fork to their left first. When this happens, assuming all of the places at the table are occupied, then all of the forks have been taken. That is, each of the five forks shown are to the left of exactly one of the five philosophers. At this point, every philosopher has exactly one fork, but there are none available for anyone to get their second fork. Unless one of the philosophers decides to give up on eating and put a fork down, all of the philosophers will starve.

Code Listing 8.24 illustrates how this scenario translates into code with semaphores. Multiple philosopher threads share an array of N fork semaphores (numbered 0 through N-1) and each thread tries to acquire two of them. Thread 0 waits on semaphores 0 and 1, thread 1 waits on semaphores 1 and 2, and so on, until thread N-1 waits on semaphores N-1 and 0 (since the modulus operator is applied).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

/* Code Listing 8.24:
   The dining philosophers problem in code with semaphores
 */

void *
philosopher (void * _args)
{
  /* Cast the args as struct with self identifier, semaphores */
  struct args *args = (struct args *) _args;
  int self = args->self;       /* unique thread identifier */
  int next = (self + 1) % SIZE;
  sem_wait (args->sems[self]); /* pick up left fork */
  sem_wait (args->sems[next]); /* pick up right fork */
  /* Critical section (eating) */
  sem_post (args->sems[next]); /* put down right fork */
  sem_post (args->sems[self]); /* put down left fork */
  /* Do other work and exit thread */
}

Assuming they are initialized to 1 and the standard sem_wait() is used, semaphores exhibit the three required system features of deadlock. They enforce mutual exclusion because the second thread to attempt to down the semaphore will become blocked since the internal value would be negative. Since the threads can acquire one and get blocked trying to acquire the second semaphore, they satisfy the hold-and-wait criterion. And since no thread can break another thread’s claim to a semaphore, the no preemption criterion is met. The fourth criterion for deadlock, circular wait, arises from the sequence in which the threads wait on the respective semaphores. Every philosopher is waiting on the fork to their right, which has been grabbed by someone else as their left fork.

Example 8.5.1

---

Table 8.1 illustrates how the circular wait arises. Every thread successfully waits on one semaphore and gets blocked by the second.

Thread 0	Thread 1	Thread 2	Thread 3	Thread 4
sem_wait(0);    SUCCESS sem_wait(1);    BLOCKED	sem_wait(1);    SUCCESS sem_wait(2);    BLOCKED	sem_wait(2);    SUCCESS sem_wait(3);    BLOCKED	sem_wait(3);    SUCCESS sem_wait(4);    BLOCKED	sem_wait(4);    SUCCESS sem_wait(0);    BLOCKED

Table 8.1: If all threads get through the first semaphore, no one gets by the second

It is important to note that this problem applies to other synchronization primitives, not just semaphores. That is, locks and condition variables also meet the system requirements for deadlock. To illustrate how this problem could arise in practice with locks, consider the software that links incoming and outgoing connections in a network switch. In this scenario, assume that each thread responsible for forwarding data packets acquires locks on dedicated physical ports. As such, the software maintains an array of locks nic_locks. There is no assumption that the ports need to be adjacent; instead, the switch code just grabs any two that are available. Code Listing 8.25 shows a simplistic approach that fits the dining philosophers structure. The first loop iterates through the locks until one is assigned to be this thread’s incoming port; the second loop acquires the outgoing port. To make matters worse, these two loops may be in different portions of the code base, so someone reviewing the code may not think they are actually connected in this way!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

/* Code Listing 8.25:
   It is easy to fall into the dining philosophers structure without realizing it
 */

while (true)
  {
    in++;
    in %= NUMBER_OF_PORTS;
    if (!pthread_mutex_trylock (nic_locks[in]))
      break;
  }
  /* successfully locked network card in for incoming data */

while (true)
  {
    out++;
    out %= NUMBER_OF_PORTS;
    if (!pthread_mutex_trylock (nic_locks[out]))
      break;
  }
  /* successfully locked network card out for outgoing data */

8.5.1. Solution of Limiting Accesses¶

One approach to solving the dining philosophers problem is to employ a multiplexing semaphore to limit the number of concurrent accesses. To return to the original metaphor, this solution would require that one of the seats at the table must always remain unoccupied. Assuming all of the philosophers try to grab their left fork first, the fork to the left of the empty seat would not be claimed. Consequently, the philosopher to the left of that seat could grab the fork as their second, as it is the fork to their left. After this philosopher eats, they can put both forks down, making their left fork available as the right fork for the next philosopher.

Code Listing 8.26 shows how to incorporate this approach into the structure of Code Listing 8.24. A single additional semaphore (can_sit) is created and initialized to N-1 for N semaphores. This semaphore prevents all N semaphores from being decremented by the first call to sem_wait(). As such, there must be at least one semaphore that can be decremented by the second call, guaranteeing one thread enters the critical section. Once that thread leaves, it increments its fork semaphores and the new semaphore, allowing a new thread to enter.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

/* Code Listing 8.26: Solving dining philosophers with a multiplexing semaphore */ void * philosopher (void * _args) { /* Cast the args as struct with self identifier, semaphores */ struct args *args = (struct args *) _args; int self = args->self; /* unique thread identifier */ int next = (self + 1) % SIZE; sem_wait (args->can_sit); /* multiplexing semaphore */ sem_wait (args->sems[self]); /* pick up left fork */ sem_wait (args->sems[next]); /* pick up right fork */ sem_post (args->can_sit); /* multiplexing semaphore */ /* Critical section (eating) */ sem_post (args->sems[next]); /* put down right fork */ sem_post (args->sems[self]); /* put down left fork */ /* Do other work and exit thread */ }

Example 8.5.2

---

At first glance, it may appear that placing the call to sem_post() before the critical section could still allow the same problem as before. Specifically, this structure allows N calls to sem_wait(), just as the original version did. However, the order of the outcomes is different, as highlighted in Table 8.2. If thread 1 was initially blocked by the multiplexing semaphore, thread 0 is able to call sem_wait(1) successfully first. This order of events breaks the circular wait.

Thread 0	Thread 1	Thread 2	Thread 3	Thread 4
sem_wait(0);    SUCCESS sem_wait(1);    SUCCESS	sem_wait(1);    BLOCKED	sem_wait(2);    SUCCESS sem_wait(3);    BLOCKED	sem_wait(3);    SUCCESS sem_wait(4);    BLOCKED	sem_wait(4);    SUCCESS sem_wait(3);    BLOCKED

Table 8.2: The multiplexing semaphore changes where threads get blocked

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

/* Code Listing 8.27:
   Solving dining philosophers with a multiplexing semaphore
 */

while (! success)
  {
    sem_wait (args->sems[self]);     /* pick up left fork */
    /* perform some initial work */
    if (sem_try_wait (args->sems[next]) != 0)
      {
        /* undo current progress if needed and possible */
        sem_post (args->sems[self]); /* drop left fork */
      }
    else
      success = true;
  }

8.5.3. Solution by Imposing Order¶

A third possibility for solving the dining philosophers problem is to impose a linear ordering on the semaphores. This order could be imposed by requiring i < j anytime sems[i] is accessed before sems[j]. As before, thread 0 would wait on semaphores 0 and 1 (in that order), thread 1 would wait on semaphores 1 and 2, and so on. However, the last thread would have a different ordering. If there are N semaphores (numbered 0 through N-1), the last thread would have to wait on semaphore 0 before semaphore N-1 to adhere to the linear ordering. Code Listing 8.28 shows how this order can be imposed by adding a single if statement.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

/* Code Listing 8.28: Enforcing a linear ordering by requiring self < next */ void * philosopher (void * _args) { /* Cast the args as struct with self identifier, semaphores */ struct args *args = (struct args *) _args; int self = args->self; /* unique thread identifier */ int next = (self + 1) % SIZE; if (self > next) swap (&next, &self); /* enforce order */ sem_wait (args->sems[self]); /* pick up left fork */ sem_wait (args->sems[next]); /* pick up right fork */ /* Critical section (eating) */ sem_post (args->sems[next]); /* put down right fork */ sem_post (args->sems[self]); /* put down left fork */ /* Do other work and exit thread */ }

Example 8.5.3

---

To visualize how this change affects the outcomes to prevent deadlock, consider the highlights in Table 8.3. Since thread 4 must adhere to the linear order, it must try to wait on semaphore 0 before it can wait on semaphore 4. Assuming thread 0 arrived earlier and decremented semaphore 0 successfully as shown, thread 4 becomes blocked from the start. Consequently, thread 3 is successful in decrementing semaphore 4. The linear ordering prevents the circular wait that would cause deadlock.

Thread 0	Thread 1	Thread 2	Thread 3	Thread 4
sem_wait(0);    SUCCESS sem_wait(1);    BLOCKED	sem_wait(1);    SUCCESS sem_wait(2);    BLOCKED	sem_wait(2);    SUCCESS sem_wait(3);    BLOCKED	sem_wait(3);    SUCCESS sem_wait(4);    SUCCESS	sem_wait(0);    BLOCKED sem_wait(4);

Table 8.3: Thread 4 gets blocked by semaphore 0, allowing thread 3 to proceed