5.4. Network Security Fundamentals¶
The previous section suggested that the length and checksum calculations in UDP and TCP headers provide rudimentary error checking. This statement should not be read to mean that either UDP or TCP provide secure data exchange in any meaningful sense. While many people talk about security in a general sense, within the domain of computer systems, security refers primarily to the ability to provide three services: confidentiality, integrity, and availability.
Confidentiality is the service that a message can be read only by an entity that is authorized to do so. Consider the case where a person named Alice has a secret to share with Bob. Alice intends that Bob is the only other person authorized to learn this information. Confidentiality is the guarantee that this goal is achieved. Confidentiality would be broken if a third person, Eve [1], could learn the secret in some way.
Integrity is the service that the communication is protected against unauthorized modifications. Returning to Alice and Bob, consider a message from Alice that authorizes a bank transfer of \$1,000 to Bob’s bank account. Integrity ensures that the bank receives the correct message. Integrity would be violated if Mallory could corrupt the message to reduce the transfer down to \$1; Bob would not get the full expected transfer and would be rather upset. Mallory could also violate integrity by increasing the amount to \$100,000 in an attempt to remove all of the money from Alice’s account; Mallory may be motivated purely by the goal of harming Alice rather than intending to help Bob. Or Mallory may try to profit off the attack by changing the account number to redirect the transfer.
Availability requires that authorized users are not prevented from performing authorized actions, whether that action involves reading or modifying data. In the first case, Mallory may break the guarantee of availability by preventing Bob from receiving the secret message that Alice sent. In the second case, Mallory might launch a denial-of-service attack against the bank to prevent it from receiving Alice’s message authorizing the transfer.
Neither TCP nor UDP provide any of these three guarantees. The contents of the application-layer payload are not hidden or scrambled in any way, so there is no guarantee of confidentiality. The checksum calculation can be trivially manipulated to break integrity without detection: change the order of the bytes in the segment. Checksums are essentially just addition, and it is a fundamental tenet of basic arithmetic that 3 + 5 and 5 + 3 produce the same result. Although TCP aims to provide reliable data transport, its services do not meet the standard required for availability. TCP’s reliability consists of trying again when an expected segment does not arrive; this second (and third…) attempt can easily fail again in a successful denial-of-service. Consequently, neither TCP nor UDP guarantee any of these security services.
Cryptography is a specialized field that uses a variety of techniques—typically advanced mathematical concepts—to create secure communication channels. This section provides a very brief overview of two cryptographic techniques that are relevant to the current discussion. Encryption involves encoding a message (the plaintext) into random-looking binary string (the ciphertext) in a way that allows the process to be reversed. Encryption, then, provides confidentiality by hiding the secret message in an unreadable way. Cryptographic hash functions, on the other hand, encode the message into a fixed-length ciphertext that does not allow the plaintext to be recovered. Cryptographic hash functions provide integrity, as they are designed to prevent adversaries from finding a corrupted plaintext that produces the same ciphertext.
Neither of these techniques guarantees availability, which is extremely difficult to provide. To illustrate an availability attack, recall the three steps of the TCP handshake. In a SYN flood, an adversary repeatedly sends SYN packets to initiate the handshake and open a connection; as each of these arrive at the server, the server allocates internal data structures to handle the request. However, the adversary never completes the handshake for any of these requests or closes the connection. Consequently, the server eventually runs out of memory or other resources, preventing legitimate users from connecting. Detecting these types of attacks is not straightforward, making availability a challenge. To make matters worse, availability is often at odds with confidentiality and integrity. Providing confidentiality or integrity can make availability more difficult, and vice versa. As our goal is to focus on the basic principles of security, we limit our discussion to the basics of encryption and cryptographic hash functions; interested readers should explore the recommended readings for more information.
5.4.1. Symmetric Key Encryption¶
The process of encryption involves combining a plaintext message with a key to create a ciphertext that looks like an unreadable series of random bits. In a perfect encryption system [2], when Alice sends a ciphertext to Bob, Eve learns nothing about the plaintext. However, Bob will be able to decrypt the message back into its plaintext form with the corresponding key.
Encryption and decryption are often written in a formal notation, using $m$ and $c$ to refer to the plaintext message and ciphertext, along with $e_K$ and $d_K$ to denote encryption and decryption functions using a particular key. This notation leads to the following generic equations:
There are two distinct styles of encryption that are in common use. In symmetric key encryption, the same key is required for both encryption and decryption. That is, Alice and Bob must have an agreement before exchanging the ciphertext of what the key is. In contrast, public key encryption uses two distinct keys for encryption and decryption. In this key pair, one (public) key can be made publicly available while the other (private) must remain secret. For instance, Alice can use Bob’s public key to encrypt a message, allowing only Bob to decrypt it using his private key. On the other hand, Alice can encrypt a message using her private key, allowing Bob or anyone else to decrypt it using Alice’s public key. This latter approach is the basic idea behind cryptographic signatures, as it provides a way to confirm that a message truly came from Alice; if the message can be decrypted with Alice’s public key, it must have been encrypted with her private key (that only she knows).
The most commonly used symmetric key cipher in modern practice is the Advanced Encryption Standard (AES). National Institute of Standards and Technologies (NIST)—a part of the U.S. federal government that defines cryptographic and other technical standards—selected AES as a replacement for older symmetric key ciphers when those were found to have weaknesses. AES uses a technique called the Rijndael block cipher, breaking the plaintext into a sequence of 128-bit blocks that are each encrypted. AES has three variations based on the length of the key (128, 192, or 256 bits long).
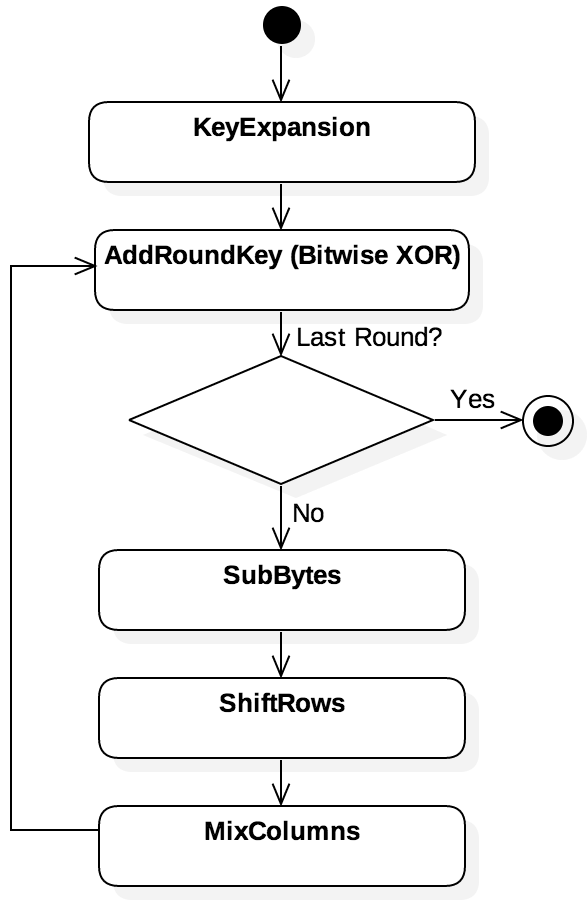
Rather than a single procedure, AES encryption is an iterative process that uses several keys—one
per round of the iteration. Figure 5.4.1 illustrates the overall structure of AES. The
original 128-, 192-, or 256-bit key is first used as the input to a KeyExpansion algorithm,
generating a key schedule of multiple round keys. Then, for each 128-bit block of the
plaintext, AES arranges the bits into a 4x4 matrix of bytes, which represents the state of the
block. Within each round, the round key is combined (AddRoundKey) with the state by applying
the bitwise XOR operation. Next, the SubBytes step replaces the contents by looking each byte up
in a substitution box (S-box); for instance, any byte that contains the value 13 might be replaced
with the value 275. The ShiftRows step rotates each row by a different number of places to the
left (e.g., row 0 stays intact, row 1 bytes shift one place to the left, and so on). The
MixColumns applies a linear transformation that mixes the placement of bits within a single
column. To decrypt an AES ciphertext, the same key schedule is used, but in reverse. The steps of
each round are also reversed.
The strength of symmetric key algorithms like AES derives from the strong probabilistic guarantees associated created by non-linear operations. For example, consider the XOR operation. If the output of a one-bit XOR operation is 1, there are two equally likely possibilities: either the plaintext bit is 0 and the key is 1, or the plaintext is 1 and the key is 0. This approach is the basis of a one-time pad, in which all of the bits of a plaintext are XORed with a random key that is the same length as the input. Under many ideal assumptions, one-time pads achieve information theoretic security, which means that an adversary trying to break the code can only guess. Every bit of the key is equally likely to be a 1 or a 0. Regardless of how long an adversary’s program runs, the probability of each bit never changes, and the program cannot make progress toward breaking the code. In essence, one-time pads are perfectly secure in theory; in practice, they are not, because the plaintext messages cannot achieve the level of randomness required. For example, assume that Eve knows Alice sent either “Hello” or “Goodbye” with a one-time pad; Eve does not need to know the key, because she can determine the message by examining just the length of the ciphertext. Hence, practical symmetric key approaches like AES combine XOR with other operations that further obscure the message.
The operations used in AES are very fast, measured on the scale of CPU cycles. The full encryption process for a single block requires 10, 12, or 14 rounds (based on the key size). Consequently, AES can encrypt a significant amount of data very efficiently. The only problem is how should Alice and Bob determine what key to use, particularly if they have never spoken before? For instance, when you use a web browser to visit your school’s or bank’s website for the first time, the browser and server need to determine a key to use. As a complicating factor, depending on more advanced characteristics of the algorithm, it may be necessary to ensure the key has not been used before.
C OpenSSL library functions – <openssl/evp.h>
This is not a standard library, so you may need to use the -I and -L compiler flags.
EVP_CIPHER_CTX *EVP_CIPHER_CTX_new (void);- Creates a new context for encryption or decryption.
void EVP_CIPHER_CTX_free (EVP_CIPHER_CTX *ctx);- Frees up resources allocated to a context.
int EVP_EncryptInit (EVP_CIPHER_CTX *ctx, const EVP_CIPHER *cipher, const unsigned char *key, const unsigned char *iv);- Initializes the context to use a cipher given a key and initialization vector.
int EVP_EncryptUpdate (EVP_CIPHER_CTX *ctx, unsigned char *out, int *outl, const unsigned char *in, int inl);- Updates the encryption computation for the plaintext chunk in, writing the results to out.
int EVP_EncryptFinal (EVP_CIPHER_CTX *ctx, unsigned char *out, int *outl);- Writes the final ciphertext into the buffer out.
Code Listing 5.2 shows the basic structure of initializing an encryption context using
the OpenSSL crypto library. [3] All symmetric key ciphers require specifying a cipher
mode. In this example, we are using cipher block chaining (CBC), a very widely used mode.
1 2 3 4 5 6 7 8 9 10 11 12 13 | /* Code Listing 5.2:
Create an encryption context for AES-256 in CBC mode
*/
/* Create REALLY BAD 256-bit key and initialization vectors. For
AES-256, key must be 256 bits (32 bytes) and initialization
vector is 128 bits (16 bytes). */
unsigned char *key = (unsigned char *) "aaaabbbbccccddddeeeeffffgggghhhh";
unsigned char *iv = (unsigned char *) "iiiijjjjkkkkllll";
/* Set up the context and initialize it */
EVP_CIPHER_CTX *ctx = EVP_CIPHER_CTX_new();
EVP_EncryptInit (ctx, EVP_aes_256_cbc (), key, iv);
|
Code Listing 5.3 illustrates how to encrypt a plaintext message using the initialized
context. EVP_EncryptUpdate() can be called repeatedly as needed for long messages. For instance,
if the plaintext consisted of a large file stored on disk, the file could be read into memory in
small chunks at a time; each chunk would then be passed to EVP_EncryptUpdate() accordingly.
Code Listing 5.3 only requires a single call on line 12, as the plaintext is short.
Line 18 writes the final result into the allocated buffer ciphertext buffer. Note that this data
is not in a printable format, so an appropriate encoding (such as Base64) will need to be used for
many applications.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | /* Code Listing 5.3:
Encrypting a string using the AES context from Code Listing 5.1
*/
char *plaintext = "Hello world";
int plain_length = 12;
unsigned char ciphertext[128];
memset (ciphertext, 0, sizeof (ciphertext));
int length = 0, cipher_length = 0;
/* Update the encryption context based on the plaintext */
EVP_EncryptUpdate (ctx, ciphertext, &length, (unsigned char *)plaintext,
plain_length);
cipher_length = length;
/* Finalize the context, which may require appending some data to
the end of the ciphertext buffer */
EVP_EncryptFinal (ctx, ciphertext + length, &length);
cipher_length += length;
EVP_CIPHER_CTX_free (ctx);
printf ("Plaintext is:\n");
BIO_dump_fp (stdout, (const char *)plaintext, plain_length);
printf ("Ciphertext is:\n");
BIO_dump_fp (stdout, (const char *)ciphertext, cipher_length);
|
Assuming OpenSSL is installed in the directories shown, we can combine Code Listings 5.2
and 5.3 into a single encrypt.c file, then can compile and run this program on macOS
as follows (Linux should not need the -L and -I flags, as OpenSSL is typically installed in
the standard locations checked by the compiler). Lines 23 and 25 use the OpenSSL BIO_dump_fp()
function to write the plaintext and ciphertext buffers out to STDOUT in a format similar
to hexdump.
$ gcc -o encrypt encrypt.c -L/usr/local/opt/openssl@1.1/lib \
> -I/usr/local/opt/openssl@1.1/include -lcrypto
$ ./encrypt
Plaintext is:
0000 - 48 65 6c 6c 6f 20 77 6f-72 6c 64 00 Hello world.
Ciphertext is:
0000 - a8 46 db 10 77 55 c8 91-18 19 22 b4 73 1a d2 fc .F..wU....".s...
Decrypting messages uses the same structure as Code Listings 5.2 and 5.3.
The only difference is the function names change accordingly, such as EVP_DecryptUpdate(). The
order of the arguments in each of these functions is identical to the encryption versions.
Bug Warning
Code Listings 5.2 and 5.3 omitted error checking on the calls to the OpenSSL library functions for simplicity. In practice, every OpenSSL function’s return type should be checked to ensure that the encryption or decryption is working successfully. Failure to do so could cause a segmentation fault and crash the program.
5.4.2. Public Key Encryption¶
Public key encryption provides a solution to the problem of key exchange. With public key encryption, one of the hosts can generate a fresh (unused) AES key, then encrypt the key with the other host’s public key. That is, Alice might generate a session key $K$ to use for AES, then send Bob the message $c = e_P (K)$, using Bob’s public key $P$. Bob can then use his secret key $S$:
Unlike symmetric key, public key encryption is not derived from operations like XOR that achieve information theoretic security. Instead, public key systems strive for semantic security guarantees that reduce the adversary to having a negligible probability of successfully guessing the key or plaintext. The notion of negligible probability means that the encryption procedure leaks a small amount of information (i.e., it provides hints to the adversary), but this leakage is so miniscule that a successful guess in a reasonable amount of time is absurdly unlikely. Given enough time (think in terms of billions of years), a successful attack is possible, but the adversary would be long dead before that point. Semantic security is created by a number of mathematical problems that are known to be difficult to solve. Some of these schemes involve advanced number theory concepts, such as elliptic curves, prime number factorization, and discrete logarithms.
To illustrate the basic idea, consider the premise of the RSA (Rivest-Shamir-Adleman) algorithm. To prepare for RSA encryption, the application chooses two large prime numbers $p$ and $q$; $p$ and $q$ remain secret, while their product $n = pq$ is made public. The public and private keys, denoted $e$ and $d$ in this scenario, are chosen to have a particular property. For any number $m$ (the plaintext message):
That is, when e and d are used as two consecutive exponents and the result is calculated modulo the (public) $n$ value, the original value $m$ is returned. In effect, $e$ and $d$ cancel each other out in modular exponentiation. Note that both $n$ and $e$ can be made public; an adversary with no knowledge of $d$ is cannot efficiently compute $m$ after observing the ciphertext $c = m^e \mod n$. Additionally, observing the ciphertext $c’ = m^d \mod n$ does not immediately reveal the value of $d$, even if both $m$ and $n$ are known.
Example 5.4.1
As a simple example of the basic functioning of RSA, consider $n = 55$ ($p = 5, q = 11$). Based on these parameters, we can let $e = 3$ and $d = 7$ (the rationale for this choice is beyond the current scope of this text). If we choose our message $m = 6$, then we can compute $m^e = 63 = 216 ≡ 51 \mod 55$. Then, $51^{7} = 897,410,677,851$, which is equivalent to $6 \mod 55$. Hence, the values $e = 3$ and $d = 7$ are inverses for modular exponentiation, given $n = 55$. We could arbitrarily consider one of these values as our private key and one to release as a public key, although their size is absurdly small. (This example could be impelemtned with 8-bit unsigned integers, whereas values in real implementations of RSA would be on the scale of 4096-bit unsigned integers.)
For completeness, this particular form of RSA should never be used in practice. Just as AES required more operations than just XOR, making RSA practical requires more work than just modular exponentiation to achieve semantic security. Our goal here is to provide an illustrative example of the key idea of public key cryptography: Posting one of the keys publicly allows anyone to encrypt a message that can only be read by someone with the corresponding private key. In contrast to symmetric key, public key encryption is extremely slow, and it is not practical for encrypting large amounts of data; however, public key encryption can protect small pieces of data, such as 128-bit session keys, to allow hosts to set up a secure communication channel.
5.4.3. Cryptographic Hash Functions¶
Both symmetric key and public key encryption focus on providing confidentiality guarantees for security. Once a message has been encrypted into ciphertext, it can only be read by someone who has the corresponding decryption key. To provide integrity, though, we need a different technique. Cryptographic hash functions serve this purpose by taking an arbitrary-length input message and running it through a compression algorithm to produce a fixed-length result.
In essence, a cryptographic hash function is a one-way function to map any input to an unpredictable bit string. Readers with a background in data structures may be familiar with the concept of hash functions as used in hash tables; for instance, a simple hash function would simply apply a modulus operation to an input value. Cryptographic hash functions are very different. Cryptographic hash functions are designed to be intentionally slow, as the goal is to avoid the discovery of collisions, two inputs that share the same hash. The avalanche effect contributes to this goal, as flipping a single bit in the input produces a very different final result.
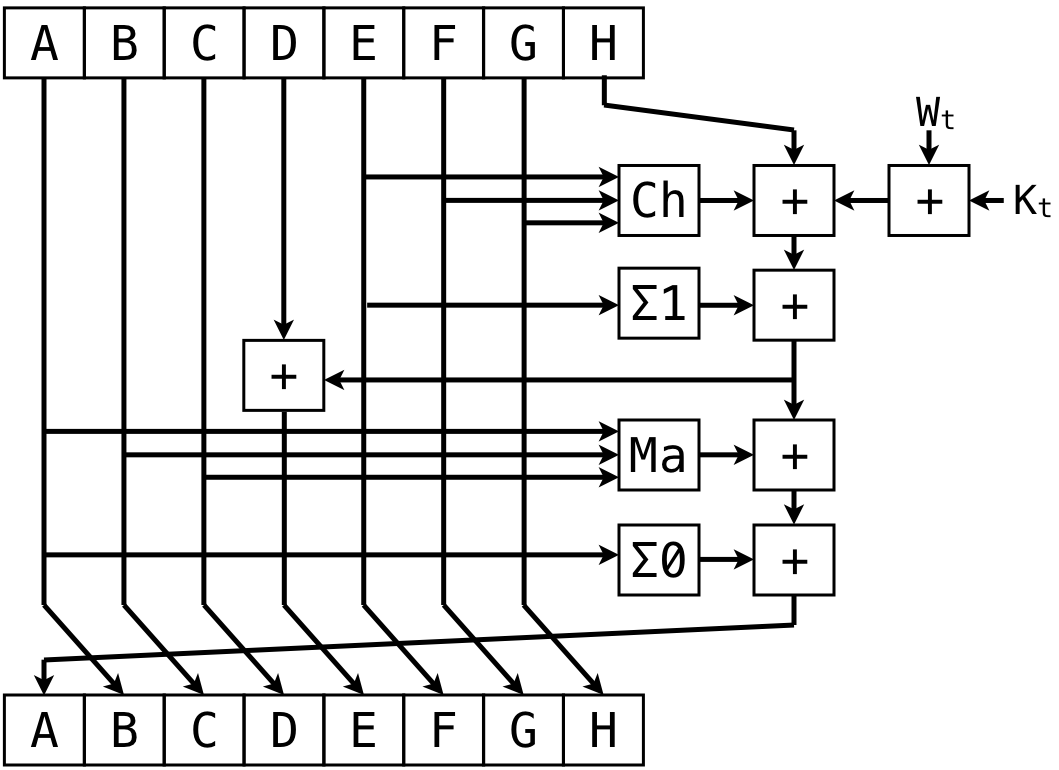
Figure 5.4.5 illustrates the compression technique used in the SHA-2, one currently recommended family of cryptographic hash functions. The message to be hashed is broken up into a series of chunks denoted as $W_t$. that are combined with a series of constants $K_t$. The running hash value—which might be 224, 256, 384, or 512 bits in length—is broken into eight smaller blocks of equal length, labeled as A-H at the top. Some blocks (A-C and E-G) are shifted to different locations (B-D and F-H) in the output. The output A and E blocks are the result of combining the eight input blocks through various operations, including XOR, bit shifting, logical operators, and one’s complement addition. The result is then fed back in to the compression algorithm; this process is repeated either 64 or 80 times, depending on the SHA-2 variant used.
Note that the compression described above only works on a single block (e.g., 256 bits) of data. The full SHA-2 procedure breaks the original, arbitrary-length message into a sequence of these blocks. At each step, the output from compressing the current block is combined with the next input block, creating a chained structure known as a Merkle-Damgård construction. The Merkle-Damgård construction is susceptible to an attack that involves extending the hash calculation with more data. That is, once the output of the cryptographic hash is computed, the adversary can continue to append more data until a collision is found.
At the time of this writing, SHA-2 is still recommended for use (unlike SHA-0 and SHA-1), as there is no known practical attack. However, given the susceptibility of the Merkle-Damgård construction to this type of attack, NIST has also released SHA-3. SHA-3 replaces the Merkle-Damgård construction with a different sponge construction. NIST recommends SHA-3 as an available alternative—not a replacement—for SHA-2, and both remain in use.
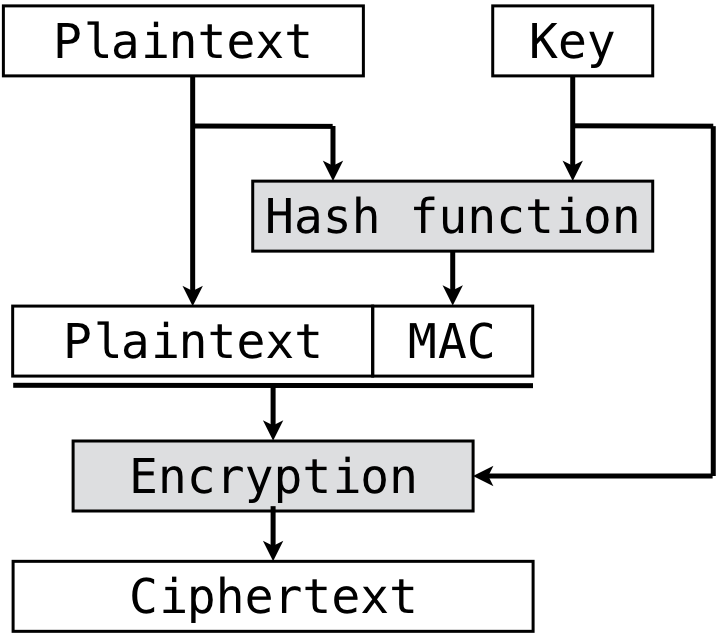
On their own, cryptographic hash functions provide a basic mechanism for integrity. If a message $m$ is known and someone claims that the hash value $H(m)$ is the correct hash value, the truth of this statement can be easily confirmed. However, that construction alone does not allow anyone to claim to be the author if $m$. Instead, the cryptographic hash function must combine $m$ with a key. Figure 5.4.6 shows one technique for doing this, known as MAC-then-Encrypt (MtE). The first step is to use a keyed cryptographic hash function that combines the plaintext with a secret key to compute a message authentication code (MAC). The MAC is then appended to the plaintext, and the resulting message is encrypted. MtE provides guarantees of both confidentiality and integrity, but it also provides a claim of authenticity about authorship—only someone with the key could generate the MAC and ciphertext.
C OpenSSL library functions – <openssl/sha.h>
This is not a standard library, so you may need to use the -I and -L compiler flags.
int SHA256_Init (SHA256_CTX *c);- Initializes a new context for SHA-256 cryptographic hash calculations.
int SHA256_Update (SHA256_CTX *c, const void *data, size_t len);- Updates the internal context for a block of data being hashed.
int SHA256_Final (unsigned char *md, SHA256_CTX *c);- Finalized the hash calculation into a message digest md.
unsigned char *SHA256 (const unsigned char *d, size_t n, unsigned char *md);- Performs all steps to hash the data in one function call. The last parameter points to a buffer used for temporary storage.
Code Listing 5.4 demonstrates how to use the OpenSSL functions for SHA-256. In this
scenario, we are assuming that the data to be hashed has been broken into several fixed-size chunks.
(If the data resides in a single block of memory, the SHA256() function performs the
initialization, calculation, and finalization of the hash value in a single call.) The context value
keeps track of the internal state of the hash over repeated calls to SHA256_Update().
1 2 3 4 5 6 7 8 9 10 11 12 13 | /* Code Listing 5.4:
Compute a single cryptographic hash over a sequence of fixed-size blocks
*/
SHA256_CTX context;
SHA256_Init (&context);
/* Assume we have several blocks that are all the same size;
update the hash value accordingly */
for (size_t i = 0; i < number_of_blocks; i++)
SHA256_Update (&context, &blocks[i], blocksize);
/* Write the hash into a byte array */
uint8_t hash[SHA256_DIGEST_LENGTH];
SHA256_Final (hash, &context);
|
5.4.4. Transport-Layer Security (TLS)¶
As we have noted previously, neither TCP nor UDP provide any security guarantees. This service is provided, instead, by Transport-Layer Security (TLS). When an application requires secure communication (denoted by attaching an “s” to a protocol name to get HTTPS, SFTP, or IMAPS), TLS is the source of that security. TLS is the successor of the secure sockets layer (SSL); due to security vulnerabilities, SSL has been prohibited by NIST since 2015 and has been removed from common applications such as web browsers. The specification for TLS 1.2 is defined in RFC 5246, while TLS 1.3 is defined in RFC 8446.
TLS works collaboratively with TCP to create secure end-to-end communication at the application layer. Consider the security needs of such a communication channel. The payload of the TCP segment needs both confidentiality and integrity, whereas the header cannot be kept confidential. To be precise, if the TCP header is encrypted, the receiving OS could not determine the port number and, as a result, the intended recipient process. Consequently, the TCP headers must remain unencrypted, but they still need to be protected from tampering.
Figure 5.4.8 shows the relationship of TCP and TLS. For example, consider a web
browser navigating to https://www.example.com instead of the standard
http://www.example.com. Recall that one difference between these two is that the HTTP request
would be delivered to port 80 at the server, whereas HTTPS would go to port 443. In both cases, the
client initiates a TCP handshake to establish the connection. After the ACK message, with standard
HTTP, the client would be expected to send an unencrypted HTTP request. With HTTPS, however, the
client’s next message must be a ClientHello that initiates a TLS handshake. The purpose
of the TLS handshake is for the two hosts to exchange information to establish a symmetric key for
encrypting messages to each other. The server replies with a ServerHello message, containing the
server’s Certificate, ServerKeyExchange, and CertiticateRequest. The client responds
with similar data until both hosts send a Finished message to indicate the TLS session has begun.
The Certificate portion of the TLS handshake messages consists of an X.509 certificate, a data structure that contains that host’s public key. The certificate, especially on the server side, is typically cryptographically signed by a certificate authority (CA). That is, a CA is a company or governmental organization that has used a keyed cryptographic hash function to sign [4] the digital equivalent of the message “This CA confirms Company X has public key 12345.” The public key in the Certificate is then used to trade the ServerKeyExchange and ClientKeyExchange messages. These messages encode information for a key exchange protocol that allows the two parties to agree on a session key. At the end of the TLS handshake, both hosts have agreed on the session key, and they use it to encrypt the payloads of the application-layer messages.
To perform the key exchange, TLS supports three approaches: a pre-shared key (PSK), Diffie-Hellman exchange (DHE), or a combination of the two (PSK with DHE). In PSK, the two hosts have been configured to use the same key. This approach is used for organizations that are under common system administration, but it does not work for two hosts that have no prior contact. Hosts with no prior contact use the DHE approach. Without delving into the details, consider the case where the two hosts determine a common message. The two hosts could come to an agreement on the key by encrypting the same message twice:
That is, assume Alice has a private key $A$ and Bob’s private key is $B$. Because the order of exponents (if this used RSA) does not matter, if Alice encrypts $m$ and Bob encrypts the result, that value would be the same as if Bob encrypted $m$ first and Alice encrypted the result. Since no one else knows the private keys, Eve cannot compute K even if she knows $m$, $e_A(m)$, and $e_B(m)$.
To protect the TCP headers, TLS computes a MAC of the original TCP header and attaches the MAC as an optional TCP field; the MAC can be computed using a number of hash functions, though SHA-2 is perhaps the most common. Attaching the MAC provides an integrity check for both hosts to know that no third party has tampered with the segment by replacing the payload contents. TLS 1.2 protected the application-layer payload using SHA-2 and AES in the MtE technique shown in Figure 5.4.8. Because MtE is not secure against attacks that reuse the ciphertext (e.g., including an old payload), TLS 1.3 has removed support for MtE and replaced it with authenticated encryption with attached data (AEAD), a technique that does the MAC and encryption in parallel in a way that avoids the ciphertext reuse threat.
In summary, TLS provides security guarantees that TCP and UDP cannot. By encrypting the application-layer payload, its contents are hidden from view while the segment traverses through the Internet. Doing so allows applications to send and receive sensitive data, such as passwords or credit card numbers; this information is only observed by the processes at the two end hosts. TLS also provides assurance that the data has not been tampered with or corrupted without detection. Ultimately, the application-layer process has no awareness that these additional calculations are being done, as TLS—like TCP—operates within the OS, returning the results to the applications after they have already been decrypted and their integrity confirmed.
5.4.5. TLS in Practice: HTTPS¶
In the previous chapter, we used the netcat utility to communicate with an HTTP server. Recall
that netcat takes two command-line arguments: a hostname and a port number. While standard HTTP
servers listen for incoming requests on port 80, HTTPS uses port 443. Given that HTTPS communicates
using the same protocol as HTTP—the only difference is that HTTPS runs on top of TLS—it is tempting
to use the same approach as before, using the different port number:
$ netcat www.example.com 443
Warning: Inverse name lookup failed for `93.184.216.34'
www.example.com [93.184.216.34] 443 (https) open
GET / HTTP/1.0
read(net): Connection reset by peer
What is not immediately obvious in print form is that the last line of this output is produced by
netcat immediately after the GET line is entered. That is, the protocol is aborted immediately
by the server and the connection is shut down. The reason for this connection loss is that port 443
is expecting a TLS handshake before any HTTP messages can be processed. Since netcat sends all
messages in an unencrypted format, it cannot be used for TLS sessions. Instead, we can use the
openssl utility (https://www.openssl.org) for this purpose. [5] The openssl
equivalent of the netcat command from above is as follows:
$ openssl s_client -crlf -connect www.example.com:443
[...almost 100 lines of immediate output...]
The first parameter indicates the openssl command to execute, as the same utility can be used to run
a TLS server, generate cryptographic keys, or many other functions. The -crlf option tells
openssl to use both '\r\n' when the user hits the enter key, and the -connect option is
used to specific the host:port combination. Once the openssl command is entered, the utility
establishes a TCP connection followed by the TLS handshake. This procedure creates almost 100 lines
of output, including specific information about the server’s certificate and how much data was
exchanged during the handshake. The last part of this output contains information such as the following lines:
SSL-Session:
Protocol : TLSv1.2
Cipher : ECDHE-RSA-AES128-GCM-SHA256
These lines indicate that the client and server have agreed to use TLS version 1.2. The key exchange protocol is the elliptic-curve version of Diffie-Hellman, using RSA for signatures. The session key will encrypt the application-layer payload using a variant of 128-bit AES in Galois/Counter Mode (GCM). Any cryptographic hashes will be computed using SHA-256, a 256-bit version of SHA-2. Eventually, the handshake messages end and the remainder of the session proceeds as follows:
[...TLS handshake messages before this point...]
GET / HTTP/1.1
Host: www.example.com
Connection: close
HTTP/1.1 200 OK
[...remainder of HTTP response and HTML code...]
closed
As before, we can enter type the HTTP messages in plaintext. In this case, we are using HTTP/1.1,
which would maintain a persistent connection. When using HTTP/1.1, the last request should include
the header line Connection: close, which closes the TCP connection after processing the request.
The HTML ends with the message closed, which indicates that the connection has been successfully
terminated.
The openssl utility encrypts and decrypts all messages without any additional work done by the
user. This behavior highlights a key strength of layered architectures: Application-layer protocols
should not have to change to adjust for transport-layer variations. Consequently, applications can
be written as before. After using connect() to create the TCP connection, the application can
invoke function calls using the OpenSSL library to perform the handshake then proceed as normal. To
be clear, this procedure is not trivial, as the developer must configure a number of options, load
valid certificates, and so on. However, once this configuration is done, all messages sent to and
received from the server will be encrypted.
| [1] | The literature of cryptography commonly uses particular names to denote certain abilities. While Alice and Bob are generic benevolent characters, the name Eve (“eavesdropper”) denotes someone attempting to learn a secret through passive observation. Similarly, Mallory (“malicious”) implies an adversary who strives to cause harm, whether through action or inaction. |
| [2] | In practice, no encryption system is perfect. Some have subtle flaws in their algorithms that create statistical patterns that can reveal hints. Others have implementation errors that leak information by taking longer or producing more heat depending on whether a particular bit of the key is a 1 or a 0. Worse still, users of the system might make errors, such as improperly re-using a key or plaintext message. During World War II, German operators re-used certain plaintext phrases, letting Polish and British cryptographers at Bletchley Park to break messages encrypted with Enigma on a daily basis. |
| [3] | OpenSSL is available at https://openssl.org and can generally be installed through OS
package managers. Documentation and code samples are available through the Wiki at https://wiki.openssl.org/. |
| [4] | It may seem circular to use a public key to sign a certificate declaring what someone else’s public key is. That is, how do we know the signature on the certificate is valid? Modern web browser and similar applications come pre-installed with the public keys for several pre-defined trusted CAs that can be used to confirm the signatures of certificates that company or organization has signed. |
| [5] | Recall that SSL was the predecessor of TLS. OpenSSL was created as an open-source SSL library; although SSL has been renamed to TLS, the library retains the OpenSSL name given that this name is widely recognized. |