9.7. Consensus in Distributed Systems¶

Distributed systems are often designed and implemented as state machines. In the state machine approach, the system contains a number of variables that can be affected by the commands that processes perform. Returning to GFS as an example, which chunk servers store a particular file chunk would constitute a state variable; sending an extra copy to another chunk server for additional redundancy would constitute a command that affects such a variable. As the processes in a distributed system are running on different—possibly physically remote—machines, the commands are performed by sending messages (including all relevant data) across the network.

The notion of state machine replication can seem very theoretical and abstract, leading to confusion. To make it a bit more concrete, consider a process running on a traditional computing system. This process includes the lines shown in Code Listing 9.11. This code opens a file and reads the first part of the contents into a buffer, then compares the bytes read in with the string indicating the location of the Python interpreter.

/* Code Listing 9.11:
   Sample code that checks if a provided file is a Python script
 */

FILE *file = fopen ("/usr/bin/smtpd.py", "r");
fread (file, buffer, sizeof (buffer));
/* Confirm the file is a Python script */
if (strncmp (buffer, "#!/usr/bin/python ", 18) != 0)
  printf ("ERROR: File is not a Python script\n");

This code implicitly relies on several pieces of information that could be considered state variables. To start, the call to fopen() needs information about the file system structure, eventually determining which exact block to read from which particular storage device. In the process, the system call required checking that the user running this program had appropriate access privileges to read from the file. More subtly, this code relies on the directory structure of the file system and the use of the '/' character to denote the directory hierarchy; in other words, there is an assumption that "/usr/bin/smtpd.py" is the name that uniquely identifies the file to be opened. The conditional check also relies on the assumption that the Python executable is present in a particular location. All of this information could be considered as part of the system state. The goal of consensus in state machine replication is to get all of the processes to agree on the values of these variables. For instance, one machine might have Python installed at /usr/local/bin/python, rather than the location shown above; this machine would be breaking the system’s consensus on where Python gets installed.

Consensus in a distributed system, then, is the notion that all of the nodes agree on a state variable’s value. To be precise, consensus is a property that may be achieved by protocols attempting to determine a variable’s value. Processes in the system exchange messages to propose values until they decide on a final value. A protocol reaches consensus by achieving three properties:

Termination: Eventually, every correct (non-failing) process decides on a value.

Integrity: If all correct processes propose the same value, then any correct process must decide on that value.

Agreement: All correct processes decide on the same value.

As an example, consider the question of whether a file chunk storing the file "foo" is being stored on a particular chunk server. A consensus protocol would provide a definitive answer to all nodes in the file system, thus allowing every user to access the file from that chunk server. As another example, consider the clock synchronization approach using NTP. Consensus would occur if all nodes in the system execute the protocol until their internal clocks have been adjusted to be identical.

9.7.1. Byzantine Generals Problem¶

The key challenge in distributed systems is the fact that processes fail. There may be intermittent delays or lost connections in the network, or software bugs may lead to crashes or other errors such as infinite loops. Even worse, some processes may be acting maliciously; someone may have joined their computer to the system for criminal or other adversarial purposes. The presence of failing processes is a defining characteristic of distributed systems, and it has implications for protocols that strive to achieve consensus.

Figure 9.7.1: Byzantine generals communicating

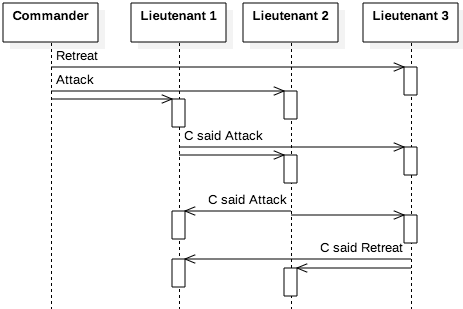
The Byzantine generals problem presents an analogy to illustrate the severity of failing processes. In its simplest form, there are three generals that each lead a part of the army of the Byzantine empire; one general is a commander and the other two are lieutenants. The three generals have surrounded a city and they are deciding whether to attack or retreat. If only one or two decide to attack, the city’s defenses are strong enough that the attackers will definitely lose. As such, either all three need to decide to attack or all three retreat. Figure 9.7.1 shows the communication for the generals. The commander sends its command to the two lieutenants, who exchange messages with each other to confirm that everyone received the same order.

If all three of the generals are loyal, then the messages X and Y would be the same. That is, if the commander decides to order an attack, the lieutenants confirm with each that the commander said to attack; similarly, if the order is to retreat, then all of the messages are the same. However, one of the generals might be treacherous and might be trying to make the Byzantine army fail. If the commander is treacherous, then message X might say to attack and Y might say to retreat; the two lieutenants then exchange conflicting messages. But if the commander is loyal and one of the lieutenants is the disloyal general, then the messages from the commander would match, but the lieutenants’ messages would conflict. From the perspective of a loyal lieutenant, both situations would appear identical.

9.7.2. Limits on Consensus¶

The Byzantine generals problem highlights a major hurdle to achieving consensus in distributed systems: misbehaving processes can prevent the correct functioning of other processes. Furthermore, because correct processes cannot have perfect information about the rest of the system, one or more processes may appear to different parts of the system as both correct and failing. To be precise, a Byzantine failure (also called a Byzantine fault) occurs when one process appears as a failure to some correct processes while also appearing correct to other processes; in a Byzantine failure, different processes have access to different, conflicting observations and cannot determine what information is reliable. As such, the system cannot determine how to respond to information from processes—which may be unreliable or faulty.

Work on the Byzantine generals problem has established a significant theoretical limitation on consensus in distributed systems. If messages cannot be authenticated and more than 1/3 of the processes fail, then it will be impossible for correct, non-faulty processes to achieve consensus with any protocol. To illustrate this insight, consider the scenarios described earlier based on Figure 9.7.1. Assume that the left lieutenant is correct and it receives the message X=attack from the commander. In the confirmation stage of the protocol, the left receives the message that “C said Retreat” from the right lieutenant. The left lieutenant is a correct process, but it cannot terminate because it cannot decide which action is the correct choice. Later work showed that this insight can be generalized for any system with 1/3 of the processes failing, for instance if there were 4 treacherous lieutenants in an army with 10 generals.

If the system can guarantee that fewer than 1/3 of the processes fail, consensus is still possible in some scenarios. To illustrate this informally, assume that there is a third lieutenant in the scenario from Figure 9.7.1, and at most one of the generals is treacherous. If the commander is loyal and orders an attack, then any loyal lieutenant will receive the order to attack along with at least one confirmation of that order; if one of the lieutenants declares “C said Retreat,” the other lieutenants can determine which general is the traitor by looking at the majority.

Figure 9.7.2: Consensus is possible even if the failing process is the commander

But consider the case where the commander is traitorous and the three lieutenants are loyal. Then two lieutenants receive the message to attack and one to retreat (or vice versa), leading to the exchange of messages as shown in Figure 9.7.2. Since the lieutenants are all loyal, they report what they received as an order accurately. Lieutenants 1 and 2 both receive three messages: “Attack” (from C), “C said Attack” (from the other), and “C said Retreat” (from Lieutenant 3). Lieutenant 3 receives “Retreat” from C along with two copies of “C said Attack” from the other lieutenants. The lieutenants can again reach consensus by looking at which order was in the majority. Interestingly, note that lieutenants 1 and 2 cannot determine which process is failing (the messages would be the same if lieutenant 3 was the disloyal general) but they can still achieve consensus.

There is a nuance that needs to be added to this conclusion, though. The Byzantine generals problem, as described above, implicitly assumes the use of synchronous communication. That is, the commander issues the orders “Do X” and “Do Y” at some time, and the lieutenants exchange confirmation messages within a particular time frame after that. In an asynchronous environment, though, the impact of failures is much worse. Without time limits on responses, processes can respond to previous messages at any time in the future. As such, when a lieutenant receives the message “C said attack,” that lieutenant cannot determine if that message is in response to the current order or to one from years ago. When asynchronous communication is involved, it is impossible for any protocol to guarantee that consensus can be reached if there is even a single failing node. In practice, there is a non-zero probability that the processes can come to an agreement, but once a single node fails, there is no guarantee that consensus is possible.

9.7.3. Practical Byzantine Fault Tolerance¶

Given that consensus is provably impossible in the presence of certain conditions, it is worth considering what level of reliable service can be accomplished by processes in a distributed system. That is, one could ask whether it is possible to gather enough reliable information to reach a probably correct answer. By applying the practical Byzantine fault tolerance (PBFT) algorithm, it is possible to reliable and efficient state replication, so long as the system maintains the property that fewer than 1/3 of the processes fail. Note that the system does not strive for consensus—which would require all correct processes to reach the same decision—but for sufficient consistency among enough responses to provide usable service.

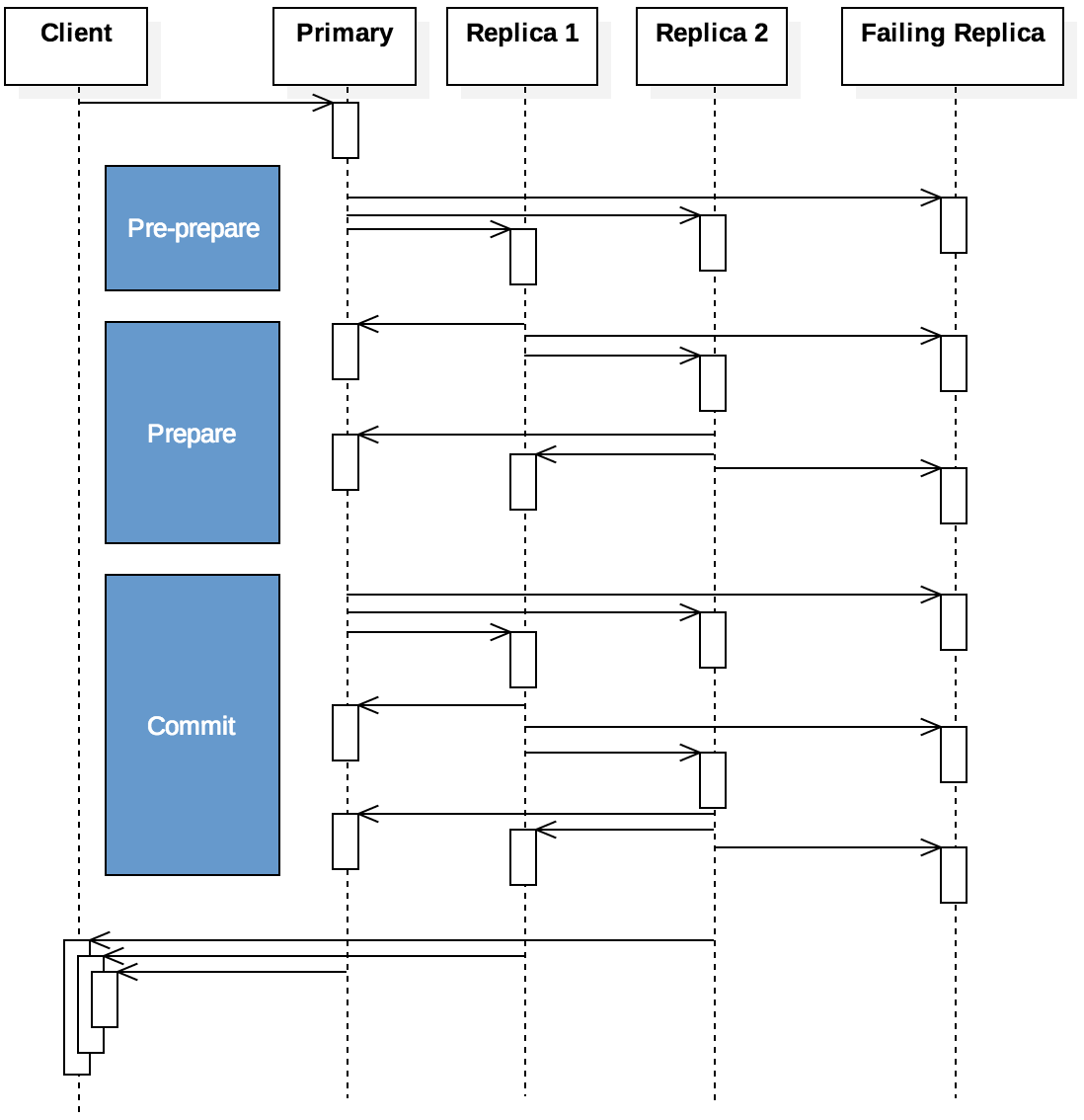
Figure 9.7.3: Reliable service with PBFT

In PBFT, a client contacts a designated primary process responsible for the requested data. The primary is assumed to be correct in the normal case, which is shown in Figure 9.7.3. The primary will then forward the request to multiple replicas that should also have the requested data. Once the client receives a response from enough processes (including the primary and the replicas), the client considers the majority response to be correct.

Figure 9.7.3 shows the stages of message exchanges in PBFT. When the primary receives a request, it enters a pre-prepare phase, alerting the replicas of a pending request. During the prepare phase, all non-faulty replicas multicast messages acknowledging the request to all other replicas and to the primary. Once the primary and replicas have received enough prepare messages, the system then enters the commit phase, when the primary sends the actual request to the replicas. The client accepts the result after receiving the responses.

There are several key elements that allow PBFT to provide reliable service. First, all messages are cryptographically signed to prevent forgeries; a faulty or malicious service cannot inject a fake message that appears to come from a correct process. Second, the pre-prepare and prepare messages include sequence information that create a total ordering on requests. When a primary receives a request from a client, it will attempt to process that request before any that come later. Specifically, the primary will not send out a pre-prepare message for a later request until the current request has been processed. Third, messages include timestamps that place a limited duration on how long a request can be pending; if the replicas take too long to respond with prepare messages, the primary will abandon the request and no commit message will be sent.

Finally, the primary requires a threshold number of processes that must respond at each stage; assuming the system guarantees $f ≤ (n-1) / 3$ faulty replicas (i.e., the system meets the requirement that at most 1/3 of the processes are failing at any given moment), then f prepare messages are required to enter the commit phase, and the client will require $f+1$ responses with the same result. This requirement matches the assumptions of the system’s behavior. If 1/3 of the system processes are failing, then 2/3 are correct and they would all agree to the same value. Once the client and/or the primary receives more than 1/3 responses that match, at least one of these responses came from a correct node and the response is probably reliable.

PBFT and similar approaches are regularly used in a variety of settings to create reliable services in unpredictable, asynchronous settings. For example, Byzantine fault tolerance algorithms are used in applications for Internet-based cloud storage providers, as well as aircraft systems that require real-time safety-critical behavior. PBFT cannot guarantee consensus, given the limitations that have been proven when Byzantine failures can occur. However, PBFT can provide a sufficiently reliable level of service for systems, so long as there are limits on the number of processes that can fail.

Note

PBFT is a fault tolerant extension to the Paxos family of consensus protocols. The goal of the Paxos protocols is to replicate a server’s state machine across multiple nodes in a distributed system. That is, instead of having a single server (which is prone to failure), the work can be spread across many machines that can continue to function even if some nodes fail. As part of this replication, it is critical for the distributed nodes to agree on the values of particular variables, such as the server’s state (e.g., running, rebooting, shutting down). The Paxos family describes how to perform this work under a variety of assumptions. PBFT, which is also known as Byzantine Paxos, is one such protocol.

A full discussion of Paxos, which is a complicated set of protocols, is beyond the scope of this book. We focused on PBFT here as an instance of how protocols can provide some level of assurance despite the impossibility result of the Byzantine generals problem. As starting resources, interested readers should consider Lamport’s “Paxos Made Simple” paper, which provides a plain-text overview of the main algorithm, or Altınbüken’s “Paxos Made More Complex” website (https://paxos.systems), which describes multiple variants and provides sample Python code. Paxos is also a standard topic for distributed systems textbooks, some of which can be found in the reading list for this chapter.