7.2. Critical Sections and Peterson’s Solution¶

Critical sections are sequences of instructions that cannot be interleaved among multiple threads. A simple example of a critical section arises when two threads share a global variable globalvar and both try to change its value with globalvar++. Recall from the previous chapter that this line of code compiles into three assembly-language instructions to load, modify, and store the result.

movq  _globalvar(%rip), %rsi    # copy from memory into %rsi register
addq  $1, %rsi                  # increment the value in the register
movq  %rsi, _globalvar(%rip)    # store the result back into memory

When multiple threads execute this code, a race condition arises since the lines can be interleaved. For instance, an interrupt during the second instruction’s execution could trigger a switch from one thread to another. Code Listing 7.1 shows the interleaved sequence of instructions (distinct indentation denotes the two threads) that would result from this unfortunate timing of the interrupt.

# Code Listing 7.1:
# A possible sequence of assembly language instructions with a race condition

# Thread A copies globalvar (5) into %rsi, adds 1 to it
movq  _globalvar(%rip), %rsi
addq  $1, %rsi

# Interrupt: Kernel switches to start running thread B

    # Thread B begins same code, also loads value of 5 into %rsi
    movq  _globalvar(%rip), %rsi
    addq  $1, %rsi
    movq  %rsi, _globalvar(%rip)
    # Thread B has copied 6 back into globalvar in memory

# Kernel later switches back to thread A

# Thread A also copies 6 back into globalvar
movq  %rsi, _globalvar(%rip)

The result of this interleaving, assuming globalvar was originally 5, is that the threads (together) performed globalvar++ twice, but the value only gets changed to 6 instead of the correct value of 7. The problem is that an interrupt occurred before the first thread was able to update globalvar, then the kernel switched to a different thread that read the old value. If this switch had not occurred until later, then the first thread would have updated globalvar with the value of 6, which is what the second thread would observe instead of the outdated 5.

It is important to note that the problem isn’t the interrupt, per se. If the interrupt occurs and the kernel switches to any other thread, or if the second thread were executing a different portion of code that had nothing to do with globalvar, the correct result would be produced. The error arises because of the combination of the interrupt/switch with the fact that both threads are accessing the same variable.

7.2.1. Peterson’s Solution¶

One approach to solving the problem of critical sections is to employ Peterson’s solution, an algorithmic approach that uses shared memory to declare intentions. Code Listing 7.2 shows the algorithm, which uses a bool array (flag) to signify a thread’s intent to enter and an int variable (turn) to indicate which thread is allowed to enter. [1]

/* Code Listing 7.2:
   Peterson's solution to solving the critical section problem
 */

flag[self] = true;
turn = other;

/* busy wait until it is safe to enter */
while (flag[other] == true && turn == other) ;

/* critical section */
flag[self] = false;

The turn variable plays a critical role in ensuring the correct functioning of the solution. Specifically, this variable makes threads adopt a polite approach to requesting access: when a thread wants to enter the critical section, it must declare that the other thread gets to go first. Since this type of variable manipulation consists of a single write to memory, it can be considered atomic. Consequently, this update does not create a race condition.

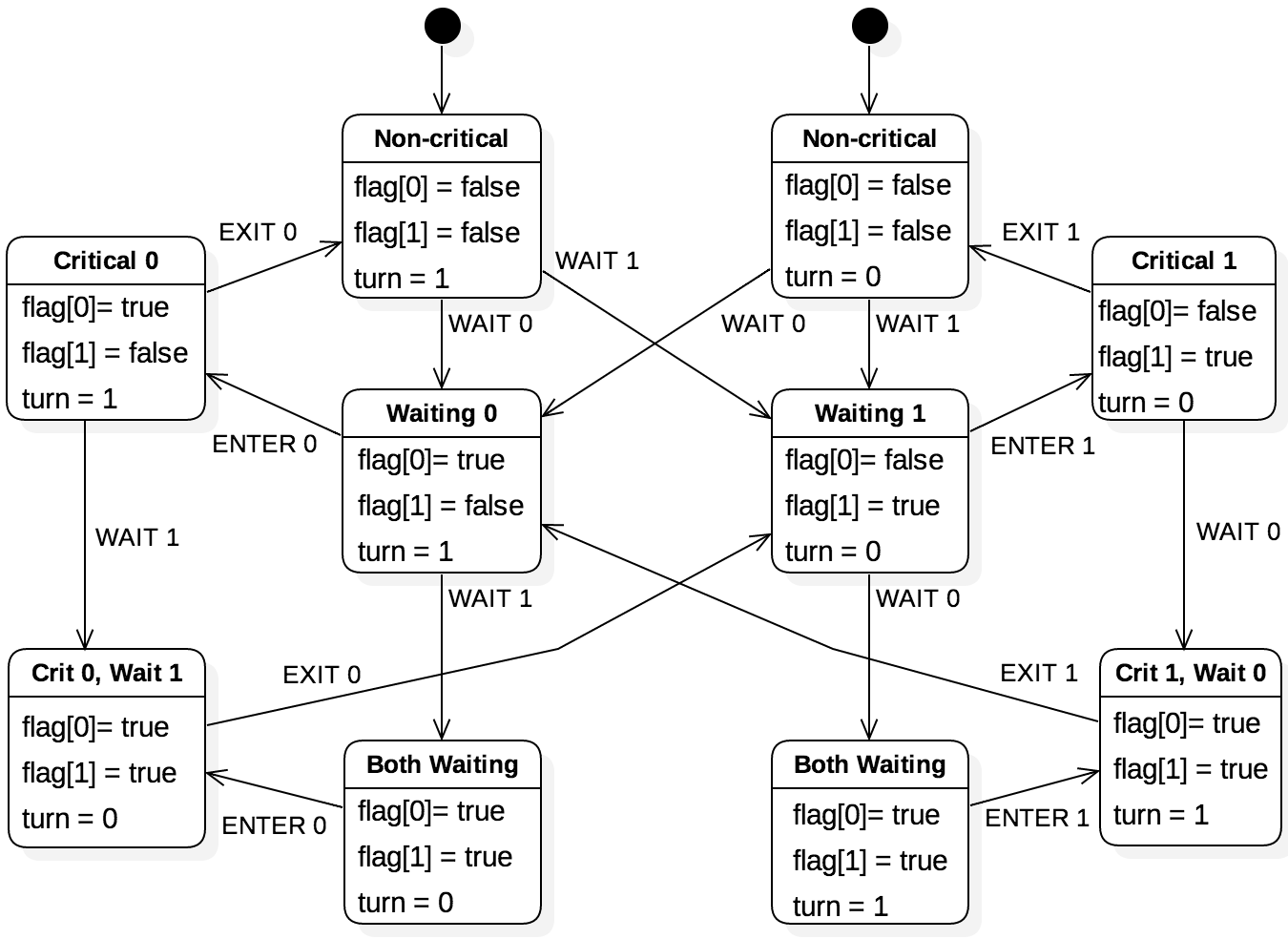
Figure 7.2.1 illustrates all possible states and transitions for Peterson’s solution. In this model, there are three basic types of events for each thread: WAIT, ENTER, and EXIT. The six states at the top of the model show the transitions when there is no contention. For example, from the left non-critical state (neither are waiting, turn = 1), thread 0 could indicate it attempts to enter the critical section with the WAIT event and immediately enters with the ENTER event. The EXIT event restores the system to the non-critical state.

Figure 7.2.1: State model of Peterson’s solution

The four states at the bottom illustrate how the algorithm handles contention. If neither thread has entered the critical section (states Waiting 0 and Waiting 1), then the turn variable determines which thread enters. That is, the condition of the while loop can only resolve to true for one of the threads, blocking the other from entering. On the other hand, one thread may already be in the critical section (states Critical 0 and Critical 1) when the other attempts to enter. In that case, the new thread is forced to wait by the turn variable. Note that Peterson’s algorithm can be extended to more than two threads, as well.

Example 7.2.1

The state model in Figure 7.2.1 can be difficult to trace. Although it would be impractical to provide a full description of all possible sequences, we can describe a basic trace that traverses through seven of the states. As before, we use indentation to denote the separate threads, with thread T0 unindented and T1 indented. Comments interspersed indicate the state and changes to relevant variables.

/* Initial state: Non-critical with turn=1 */
flag[0] = true;
turn = 1; /* Change to Waiting 0, turn=1 */
    flag[1] = true;
    turn = 0; /* Change to Both waiting, turn=0 */

/* Both are waiting, so turn is the tie-breaker */
while (flag[1] && turn == 1) ;     /* FALSE, turn=0 */
    while (flag[0] && turn == 0) ; /* TRUE, T1 blocked */

/* Enter Critical 0, Waiting 1
   Thread 0 does critical work here */
flag[0] = false; /* Enter Waiting 1, turn=0 */

    while (flag[0] && turn == 0) ; /* FALSE, flag[0] now false */
    /* Enter Critical 1
       Thread 1 does critical work here */
    flag[1] = false; /* Enter Non-critical with turn=0 */

In this trace, both threads begin in non-critical code with neither attempting to enter a critical section until T0 executes line 2. T1 then declares its intention to enter on line 4. Lines 3 and 5 are the key events to control the ordering; whichever thread sets turn last loses the rase. Since T1 changes turn after T0 does, T0 will be the thread to enter the critical section. To confirm this fact, check the while-loop conditions on lines 8 and 9. On these lines, flag[0] and flag[1] are both true. The condition then rests exclusively on turn. Later, after T0 leaves the critical section (line 13), T1’s while-loop condition changes because flag[0] is now false; this change allows T1 to break out of the loop and continue into the critical section.

7.2.2. Synchronization Properties¶

Peterson’s solution provides three desirable properties for solutions to synchronization problems:

Safety – There is no way for two threads to be in the critical section concurrently, so they cannot interfere with each other. This property is also called mutual exclusion.

Liveness – If no thread is in the critical section and at least one tries to enter, then one of the threads will be able to enter. This property is also called progress.

Fairness – Assuming neither thread can remain in the critical section indefinitely, if a thread attempts to enter the critical section, it will eventually do so. This property is also called bounded waiting.

Examining Figure 7.2.1 provides informal assurance that these properties hold. Safety is achieved, because no state allows both threads to be in the critical section at any time. Liveness is supported by the fact that all of the waiting states have a transition defined for an ENTER event; liveness could only be broken if the system could get stuck in a waiting state. Fairness is somewhat more difficult to observe, but arises from the Crit M, Wait N states in which one thread is in the critical section and the other is trying to enter. All possible sequences of events from these states must pass through a state in which the waiting thread gets to enter. Thus, no thread that tries to enter the critical section can be infinitely blocked from doing so.

The combination of all three of these properties is very difficult to achieve for synchronization problems. Generally speaking, safety is a requirement and no approach would be considered a solution without guaranteeing mutually exclusive access. Liveness is also a standard requirement; approaches that make it possible to enter a deadlock state that blocks all threads from entering the critical section are also not considered viable solutions.

In contrast, fairness is quite often difficult to achieve in practice and may even be unnecessary. For instance, consider a system that picks randomly between threads that are waiting to enter. In addition, assume that each thread will immediately try to enter the critical section after leaving it. It is theoretically possible that one thread might be extremely unlucky and never gets picked. If the choice truly is randomly distributed, this outcome would be as likely as flipping a coin and getting the same result every time. It is theoretically possible, but unlikely to happen in practice.

This scenario highlights a key misunderstanding of the liveness property. If there are no threads in the critical section and one tries to enter, there is no guarantee that thread will actually be the one allowed in. Rather, without the fairness property, it may be possible for another thread to come along and enter without waiting. To illustrate this point, consider the approach shown in Code Listing 7.3. This code meets the safety and liveness properties by permanently blocking out one of the threads.

/* Code Listing 7.3:
   An approach that guarantees safety and liveness but not fairness 
 */

if (thread == 0)
  while (1) ; /* thread 0 waits infinitely */

/* enter critical section */

7.2.3. Peterson’s Solution and Modern Hardware¶

The elegance of Peterson’s solution makes it an interesting approach that provides these three key properties. However, this approach is generally not used in modern systems. Peterson’s solution rests on the assumption that the instructions are executed in a particular order and memory accesses can be achieved atomically. Both of these assumptions can fail with modern hardware. Due to complexities in the design of pipelined CPUs, the instructions may be executed in a different order. Additionally, if the threads are running on different cores that do not guarantee immediate cache coherency, the threads may be using different memory values.

Although there are hardware mechanisms available to overcome these issues, Peterson’s solution also suffers from its lack of abstraction. From the systems programmer’s perspective, it is more desirable to use abstractions such as locking and unlocking a critical section rather than setting memory bits. As such, the remainder of this chapter will focus on higher-level abstractions and techniques that facilitate more robust and adaptable solutions, called synchronization primitives, to these types of problems. In general, these primitives fail to guarantee fairness and thus cannot provide the same theoretical properties of Peterson’s solution. However, their higher level of abstraction provides greater clarity in their practical use.

[1]	The standard explanation of Peterson’s solution uses 0 and 1 to refer to the two threads, respectively. Here, we adopt a higher level of abstraction, using `self` and `other` to refer to the two. For thread 0, `self` would be 0 and `other` would be 1; the reverse is true for thread 1.