c-Polyhedra
Start with a triangulation $T$ of a topological sphere. Label each edge $uv$ of $T$ with a positive real weight $w(uv)$. Now, suppose for each vertex $v$ of $T$ we draw a circle $c_v$ on the unit sphere such that for each edge $uv$ of $T$ the inversive distance between $c_u$ and $c_v$ is $w_{uv}$. The resulting pattern of circles is the c-polyhedron $C_T$. We say that $C_T$ realizes $(T, w)$.
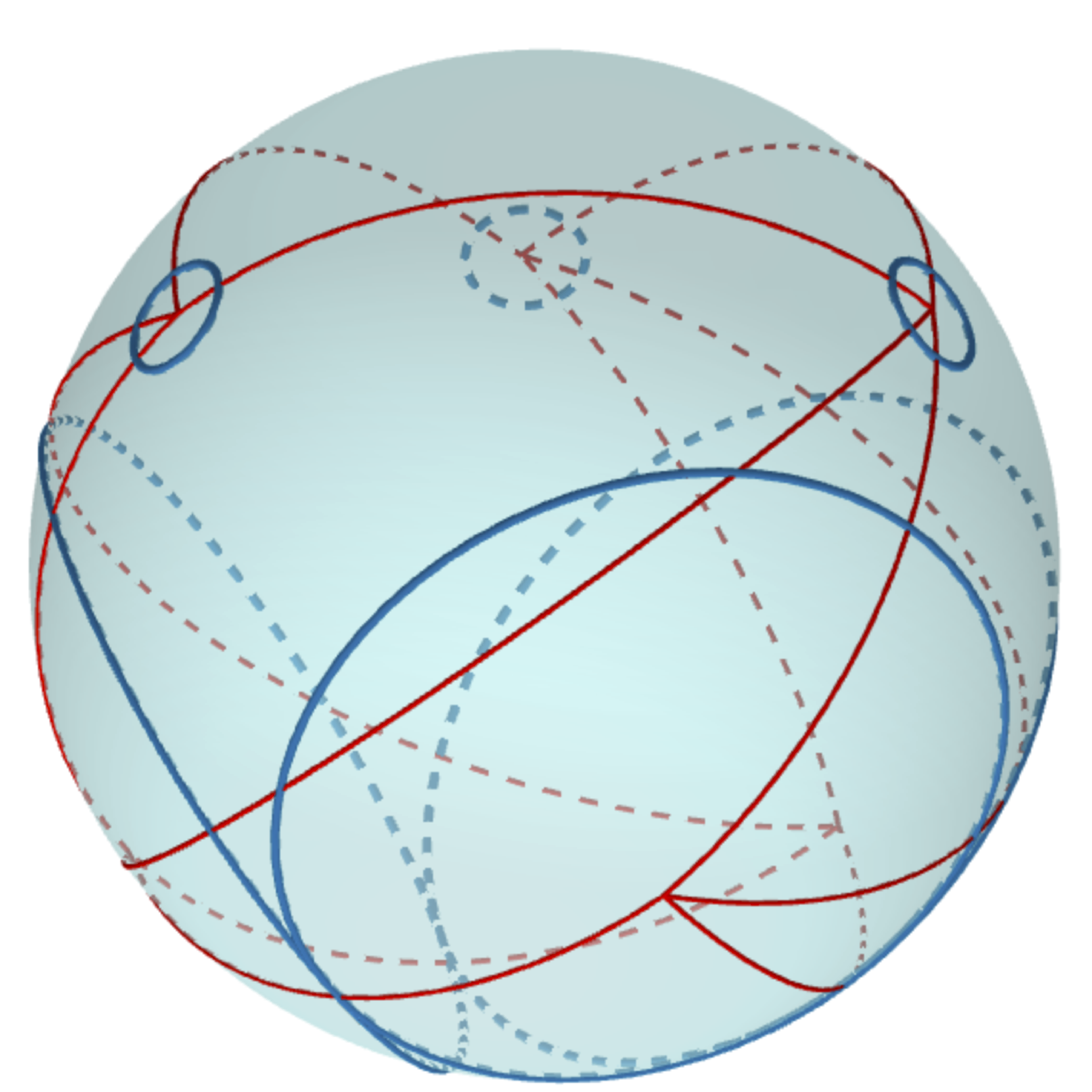
One interesting question is on the uniqueness of c-polyhedra. If we fix $T$ and the weight function $w$, are all of the c-polyhedra realizing $T$ equivalent up to Möbius transformations on the sphere? Somewhat surprisingly, this turns out to be false, even though similar uniqueness results are true if we switch our domain from the sphere to either the plane or hyperbolic space! Ma and Schlenker showed this originally using some sophisticated and beautiful geometric tools (Pogorolov maps and de Sitter space) [3]. They gave a construction for generating two different c-polyhedra with the same underlying weighted triangulation $(T, w)$ that were not Möbius equivalent. Subsequently, we found many examples using only elementary spherical geometry. One such example is based on insights obtained from reading [3], which we call Ma-Schlenker octahedra. Figure 1 shows an example. The circles are drawn in blue and the triangulation is drawn in red. See the software section below for Mathematica notebooks we created to generate examples for [1].
Software
- Elliptical Ma-Schlenker c-Octahedra. This visualization is a companion to [1]. It allows for various Ma-Schlenker octahedra with elliptical flow to be generated and analyzed.
- Hyperbolic Ma-Schlenker c-Octahedra. Coming soon.
- Parabolic Ma-Schlenker c-Octahedra. Coming soon.
Papers
- [1] J. C. Bowers and P. L. Bowers. Ma-Schlenker c-Octahedra in the 2-sphere. Preprint. June, 2016.
Talks
- [2] J. C. Bowers*, P. L. Bowers, and K. Pratt. Cauchy rigidity of convex $c$-polyhedra. ICERM Workshop on Unusual Configuration Spaces. September, 2016. Providence, RI, USA. Video
- [3] J. C. Bowers* and P. L. Bowers. Non-globally rigid inversive distance circle packings. ICMS Workshop on Geometric Rigidity Theory and Applications. June, 2016. Edinburgh, UK. (slides)
Other references
- [4] J. Ma and J.-M. Schlenker. Non-rigidity of spherical inversive distance circle packings. Discrete & Computational Geometry, 47(3):610–617, Feb. 2012.
Colleagues and collaborators
- Philip L. Bowers (The Florida State University)
- Brittany Braswell (James Madison University)
- Xiang Chen (James Madison University)
- Gregory Dreifus (Oak Ridge National Labs)
- Kevin Pratt (University of Connecticut)
- Don Sheehy (University of Connecticut)
- Ken Stephenson (The University of Tennessee Knoxville)