

|
Surfaces
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
Surfaces
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |





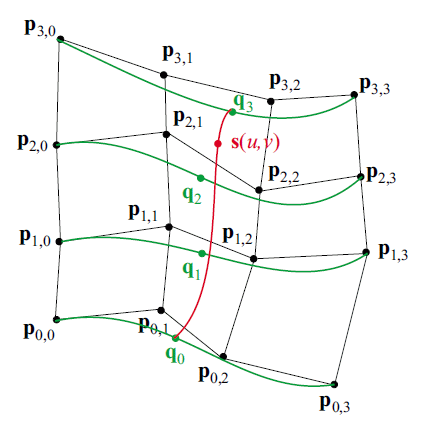






\( \bs{s}(u,v) = \left[ \begin{array}{c} \bs{v}^T (\bs{G}^T \bs{P}_1 \bs{G}) \bs{u} \\ \bs{v}^T (\bs{G}^T \bs{P}_2 \bs{G}) \bs{u} \\ \bs{v}^T (\bs{G}^T \bs{P}_3 \bs{G}) \bs{u} \\ \end{array} \right] \)

