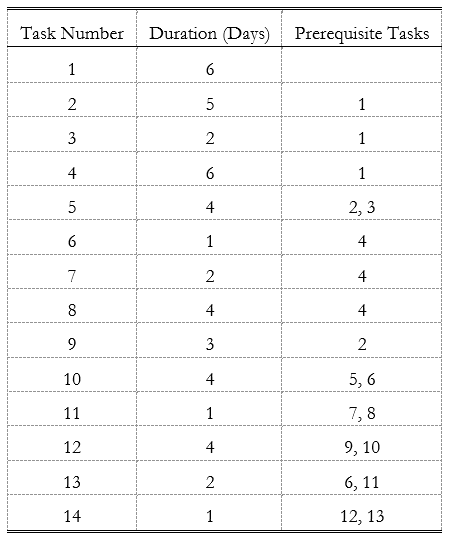
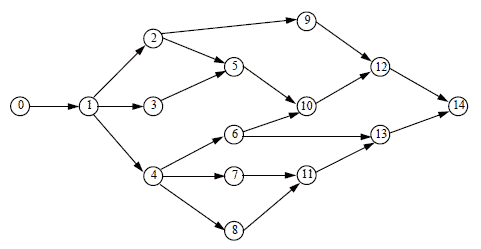
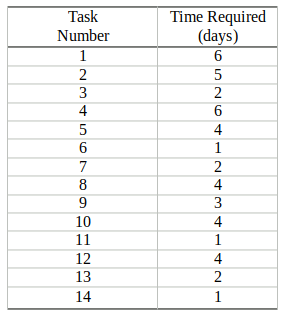
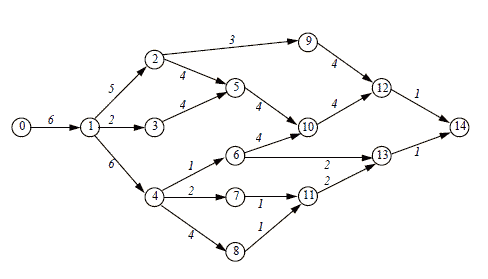
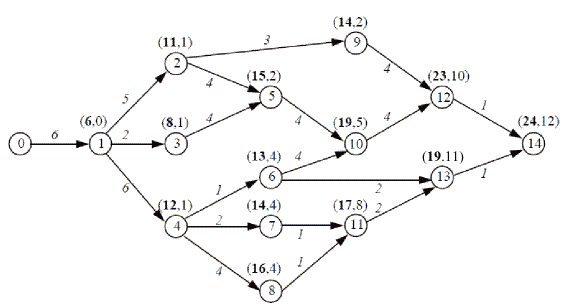
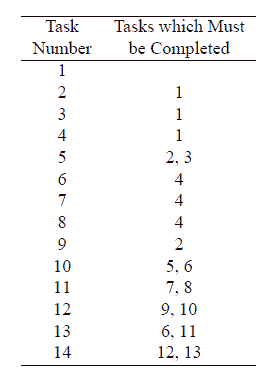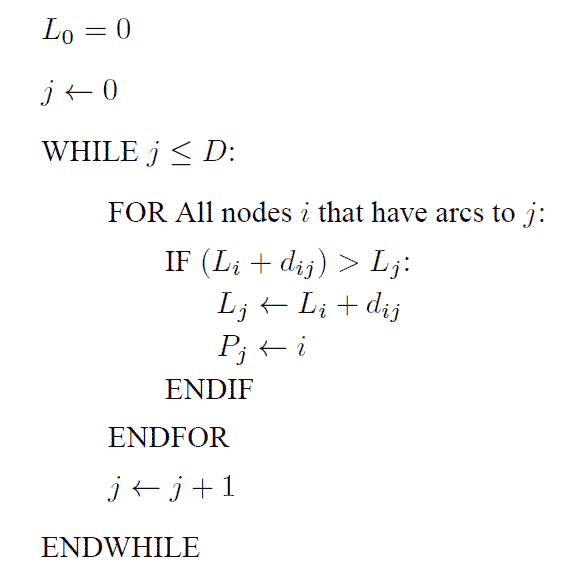|
Program Evaluation and Review Technique (PERT)
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |