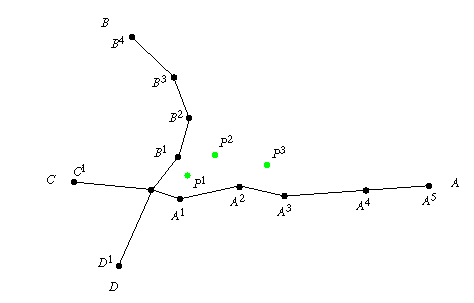
There are a number of ways to solve the map matching problem, the demonstration below uses one simple approach. Perhaps the best way to explain the algorithm is with the simple example shown below:

In this example, the person started at P⁰, the intersection of arcs A, B, C, and D (where A⁰ = B⁰ = C⁰ =D⁰). Then, three positions were recorded, P¹, P², and P³. We want to determine the distances between the piecewise-linear curve formed by connecting P⁰ ... P³ and A, B, C, and D, respectively.

The initial steps in the process are illustrated in the following Figure. First, a piecewise-linear curve is constructed by connecting P⁰, P¹, P², and P³. Then piecewise-linear curves of equal length are constructed along all of the arcs emanating from this same intersection. (For simplicity, we limit our attention only to arcs A and B.)

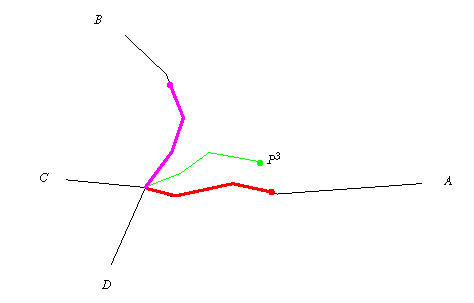
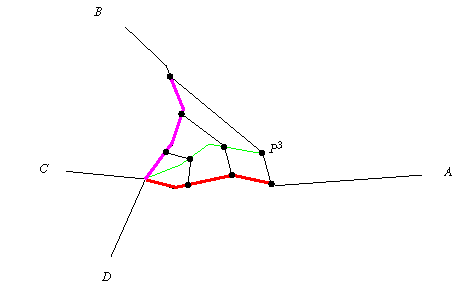
Next, as shown in the Figure below, each of the piecewise-linear curves is divided into s segments of equal length. (In this example, s=3.) Finally, the relevant distances are calculated. In this example, arc A is clearly the closest and P³ is matched to it.

This demonstration simulates a vehicle driving around on a street network. The vehicle is equipped with an AVL system that provides it with its approximate location. In this demonstration:

• The red dot represents the vehicle's actual location.
• The green dot represents the locations generated by the AVL system. The green dot is not coincident with the red dot because of errors inherent in most AVL systems.
• The blue dot represents the position of the vehicle as estimated by the map matching algorithm.

As you can see, even the "matched" locations are not perfect. This is because the algorithm being used in this demonstration has been kept extraordinarily simple. Even so, the "matched" locations are generally much better than the raw locations provided by the AVL.