Most route-finding systems use some notion of "generalized cost" to compare different routes. This cost usually includes such things as: gasoline costs, tolls, and travel time. The travel time is usually converted to a dollar cost by multiplying it by a constant "value of time".
The problem with this approach is that people generally value time nonlinearly. For example, one minute may be worth only a penny but 10 minutes may be worth $1 and an hour may be worth $15.
Why are these kinds of nonlinearities ignored? Because they make the path cost nonadditive (i.e., the cost on a path is not simply the sum of the costs on the arcs in that path) and existing algorithms for finding best paths require that the costs be additive.
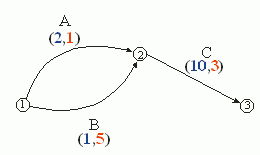
Consider the simple network shown below in which the red numbers next to the links represent travel times (in hours) and the blue numbers tolls (in dollars). Suppose that a driver traversing the network has a quadratic value of time function.

The least cost route from node 1 to node 3 uses arcs B and C; it has a total travel cost of $129. One would expect, then, that the cheapest path from 1 to 2 would also use arc B. However, arc A is the minimum cost route between nodes 1 and 2 since its total cost is $5, while the cost on arc B is $6.
This violates what is known as Bellmann's Principle of Optimality -- that the best path to any destination is comprised of the shortest path to each of the preceeding nodes on the path. Because of this violation of the optimality principle, we cannot use the existing shortest path solvers to find our optimal path.
A number of resources that consider this problem are currently available on this site, including:
For information about a particular project, feel free to contact the relevant faculty/students directly.