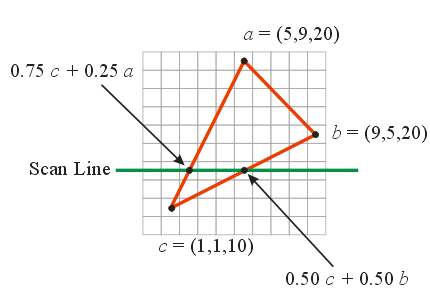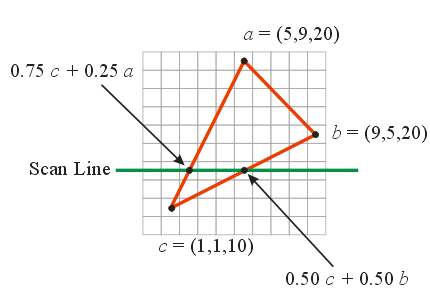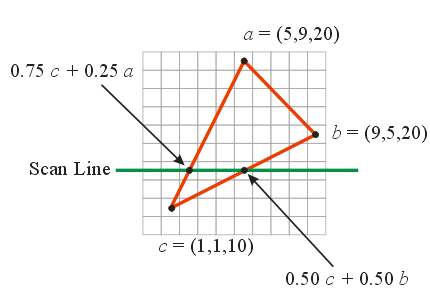Sample 3D Graphics Questions

Answer each of the following:
1. Calculate \([5 \; 2]^{\perp}\).
2. Convert the point \([5 \; 2 \; 8 \; 1]^T\) from homogeneous coordinates to Cartesian coordinates.
3. Convert the point \([4.0 \; 2.0 \; 1.0 \; 0.5]^T\) from homogeneous coordinates to Cartesian coordinates.
4. Convert the point \([-1 \; -7 \; -3]^T\) from Cartesian coordinates to homogeneous coordinates.
5. Project the 3D (homogeneous) point \([5 \; 2 \; 8 \; 1]^T\) onto the plane \(z = 10\) using an orthographic projection. Note: Do not translate or rotate the point before projectng.
6. Project the 3D (homogeneous) point \([5 \; 2 \; 8 \; 1]^T\) onto the plane \(z = 0\) using a perspective projection with a center of projection at \([0 \; 0 \; -2]^T\). Note: Do not translate or rotate the point before projectng.
7. Suppose, at a particular point, the light source direction vector is given (in 3D Cartesian coordinates) by \(\bs{l} = [1 \; 0 \; 0]^T\) and the normal direction vector is given by \(\bs{n} = [0.000 \; 0.707 \; 0.707]^T\). Compute the reflection vector for a perfectly reflective surface. Show all of your work.
8. Suppose, at a particular point, the light source direction vector is given (in 3D Cartesian coordinates) by \(\bs{l} = [1 \; 0 \; 0]^T\) and the viewer direction vector is given by \(\bs{v} = [0 \; 1 \; 0]^T\). Compute the halfway vector. Show all of your work.
Given a plane defined by the three Cartesian points \(\bs{a} = [1 \; 0 \; 0]^T\), \(\bs{b} = [0 \; 1 \; 0]^T\), and \(\bs{c} = [0 \; 0 \; 1]^T\):
1. Find a vector that is perpendicular/orthogonal to this plane. Show all of your work. Note: Your answer need not have a norm of 1.
2. Determine whether the points \(\bs{p} = [10 \; 10 \; 0]^T\) and \(\bs{q} = [2 \; 0 \; 0]^T\) lie on the same side of this plane. Show all of your work.
Use the following shear matrix: \( \left[ \begin{array}{r r r r} 1.0& 0.5& 0.5& 0.0 \\ 0.0& 1.0& 0.0& 0.0 \\ 0.5& 0.5& 1.0& 0.0 \\ 0.0& 0.0& 0.0& 1.0 \end{array}\right] \)
to transform the point:
\( \left[ \begin{array}{r} 10.0 \\ 20.0 \\ 4.0 \\ 1.0 \end{array}\right] \)

Given working versions of the following functions:

    getRotationAroundX(double phi)

    getRotationAroundY(double theta)

(each of which returns an appropriately sized Matrix), complete the following trimetricView() function.

    /**
     * Transforms the given triangle so that it will be rendered using 
     * a trimetric view. All points are in homogeneous coordinates.
     *
     * @param phi    The rotation around the x axis
     * @param theta  The rotation around the y axis
     * @param p      The points
     * @return       The transformed points
     */
    Matrix<4,3> trimetricView(double phi, double theta, Matrix<4,3> p)
    {






















    }

In binary space partitioning, when all of the vertices of a triangle are not on the same side of the plane, we split the triangle into three pieces. Explain why we split it into three pieces and not two pieces.

Given the following five 2D (Cartesian) points: \( \bs{P} = \left[ \begin{array}{r r r r r} 10 & 7 & 20 & 30 & 1 \\ 5 & 7 & 3 & 30 & 15 \end{array}\right] \)

and the following add() method (in pseudo-code):

      add(Point p, Node n)
      {
          if (p isRightOf n.point)
          {
              if (n.right == null) n.right = new Node(p)
              else                 add(p, n.right) 
          }
          else
          {
              if (n.left == null)  n.left = new Node(p)
              else                 add(p, n.left) 
          }
      }

draw the binary space partitioning tree that would be generated by the following "main" method (in pseudo-code):

      root = new Node(point[0])

      for (i = 1...N-1)
      {
          add(point[i], root)
      }

Calculate the \(z\)-value at each relevant pixel on the scan line in the following triangle.
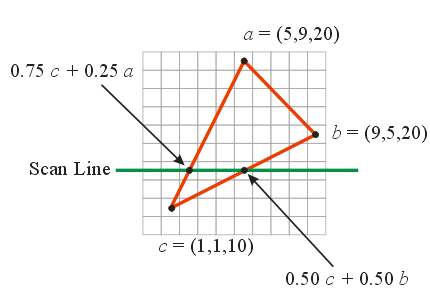
Explain Lambert's Law and how it can be used to model diffuse reflection.
Using the following lighting model: \(I = 2 \cos \theta\)
and assuming the light source is at the point \(\bs{s} = [0 \; 10 \; 30 ]^T\) and the normal vectors at \(\bs{a}\) and \(\bs{c}\) are given by:
\(\bs{n_a} = [0.577 \; 0.577 \; 0.577 ]^T\)
\(\bs{n_c} = [0.904 \; 0.301 \; 0.301 ]^T\)
calculate the light intensity for all of the relevant pixels on the scan line in the following triangle line using Gouraud shading.