Overview
Seam carving is a content-aware image resizing technique for changing the size of an image by one pixel of width or height at a time. It is a core feature in Adobe Photoshop and other graphics applications. The underlying algorithm is simple and elegant, but the technique was not discovered until 2007 by Shai Avidan and Ariel Shamir. Here is their original video presentation from SIGGRAPH 2007, the premier conference for computer graphics research:
Objectives
- Manipulate 2D arrays of objects and integers.
- Validate arguments by throwing exceptions.
Provided Files
- HJoceanSmall.png – real image
- Main.java – example application
- Picture.java – for loading images (originally found at https://introcs.cs.princeton.edu/java/stdlib/Picture.java)
- ProvidedCode.java (find this in your Canvas course) – partial solution
- SeamCarver.java – stubs
Acknowledgements
This assignment is based on materials by Josh Hug, Maia Ginsburg, and Kevin Wayne.
Example Use
Given an image, it is sometimes desirable to resize it in only one dimension. Consider the 507 pixel wide by 285 pixel tall image below. Suppose that we’d like to resize it to 357 x 285 pixels (i.e., making it narrower without changing the height).
Example 1

Original
The easiest approaches are to rescale the image or to crop the image. However rescaling ruins the aspect ratio, making everything look squashed, whereas cropping removes image content (like the people on the right).
Example 2 Rescaled |
Example 3 Cropped |
By contrast, seam carving resizes images in a content-aware manner, resulting in much better results for some types of images. Unimportant pixels (like the ocean separating the two people in the middle) are thrown away, while interesting pixels (like the people and the island) are preserved.
Example 4 Original |
Example 5 Seam Carved |
How It Works
Despite its power and modernity, the seam carving algorithm is elegant and easy to describe. We start by converting an image to an “energy matrix” using a very simple function that gives higher (brighter) energy values to important pixels and lower (darker) energy to unimportant ones.
Example 6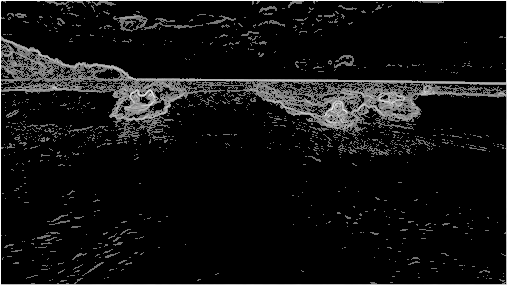 Energy of Original Image |
We then find the path from the top to the bottom such that the total energy of the path is minimized. This can be done using a dynamic programming approach or by casting it as a shortest paths problem on a directed graph. (You’ll learn about these more advanced techniques in CS 327 and CS 412.)
Example 7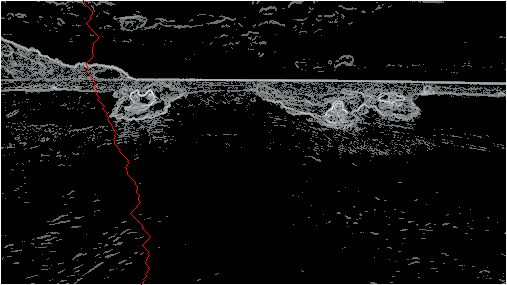 Minimum Energy Vertical Seam |
We then “shrink” the image by creating a copy of the original image, but excluding all of the seam pixels (highlighted in image above). Since the seam is exactly one pixel per row, the resulting image is one pixel narrower.
To shrink the image further, we repeat the entire process as many times as we’d like, reducing the width by one each time. Finding and removing horizontal seams is analogous.
Image Library
To read, write, and display images, we will use the Picture class from Sedgewick’s and Wayne’s standard libraries.
Within an image, the pixel (x, y) refers column x and row y.
Pixel (0, 0) is at the upper-left corner, and pixel (W-1, H-1) is at the bottom right corner.
| (0, 0) | (1, 0) | (2, 0) |
| (0, 1) | (1, 1) | (2, 1) |
| (0, 2) | (1, 2) | (2, 2) |
| (0, 3) | (1, 3) | (2, 3) |
Warning: this “column-major” order is the opposite from the mathematical notation used in linear algebra, where (i, j) refers to row i and column j. It’s also different from Cartesian coordinates, where (0, 0) is at the lower-left corner.
Colors
Each pixel is represented by a java.awt.Color object. Colors are based on three integers (ranging from 0 to 255) that represent the amounts of Red, Green, and Blue (also known as RGB values).
You can look for color charts on the web to see your favorite colors represented in values specific enough for computers. There are different systems for representing colors, but the 3-channel R.G.B. representation with values ranging from 0-255 (inclusive) is quite popular. Marketing departments often publish “Branding” guidelines to help standardize an organizations presentation on the web, in print, and etc. See for example JMU’s Branding Identity Colors page, just one component of our overall Brand Guide.
SeamCarver
In this assignment, you will implement the seam-carving technique.
The main algorithm involves three steps: (1) compute the energy of each pixel, (2) find the seam with the least amount of energy, and (3) remove all the pixels along the seam.
Step 2 has already been implemented for you in the ProvidedCode class.
Your task is to implement the SeamCarver class in the UML diagram below.
classDiagram class SeamCarver SeamCarver: -Picture picture SeamCarver: -int width SeamCarver: -int height SeamCarver: +SeamCarver(picture Picture) SeamCarver: +getPicture() Picture SeamCarver: +getWidth() int SeamCarver: +getHeight() int SeamCarver: +energy(x int, y int) int SeamCarver: +energyMatrix() int[][] SeamCarver: +removeHorizontalSeam(seam int[]]) SeamCarver: +removeVerticalSeam(seam int[])
energy
For this assignment, we will use the “dual-gradient” energy function:
- The energy of a pixel at (x, y) is Δx2 + Δy2.
- The square of the x-gradient Δx2 = Rx2 + Gx2 + Bx2. The square of the y-gradient Δy2 = Ry2 + Gy2 + By2
- Rx, Gx, and Bx are the differences of red, green, and blue components between pixel (x + 1, y) and pixel (x − 1, y).
- Ry, Gy, and By are the differences of red, green, and blue components between pixel (x, y + 1) and pixel (x, y − 1).
By convention, the indices x and y are integers between 0 and W − 1 and between 0 and H − 1 respectively, where W is the width of the current image and H is the height.
Your method should throw an IndexOutOfBoundsException if either x or y is outside its range.
When x is out of bounds, the error message of the exception should be “x = %d, width = %d” (with the specific values).
When y is out of bounds, the error message of the exception should be “y = %d, height = %d” (with the specific values).
To handle pixels on the borders of the image, we will define the leftmost and rightmost columns as adjacent and the topmost and bottommost rows as adjacent. For example, to compute the energy of a pixel (0, y) in the leftmost column, we use its right neighbor (1, y) and its left neighbor (W − 1, y).
Consider [the 3-by-4 image](the 3-by-4 image) with RGB values shown in the table below:
| (255, 101, 51) | (255, 101, 153) | (255, 101, 255) |
| (255,153,51) | (255,153,153) | (255,153,255) |
| (255,203,51) | (255,204,153) | (255,205,255) |
| (255,255,51) | (255,255,153) | (255,255,255) |
-
Non-border pixel example
The energy of pixel (1, 2) is calculated from pixels (0, 2) and (2, 2) for the x-gradient:
Rx = 255 − 255 = 0,
yielding Δx2 = 02 + 22 + 2042 = 41620.
Gx = 205 − 203 = 2,
Bx = 255 − 51 = 204,
The energy of pixel (1, 2) is calculated from pixels (1, 1) and (1, 3) for the y-gradient:
Ry = 255 − 255 = 0,
yielding Δy2 = 02 + 1022 + 02 = 10404.
Gy = 255 − 153 = 102,
By = 153 − 153 = 0,
Thus, the energy of pixel (1, 2) is 41620 + 10404 = 52024.
-
Border pixel example
The energy of the border pixel (1, 0) is calculated by using pixels (0, 0) and (2, 0) for the x-gradient:
Rx = 255 − 255 = 0,
yielding Δx2 = 02 + 02 + 2042 = 41616.
Gx = 101 − 101 = 0,
Bx = 255 − 51 = 204,
The energy of the border pixel (1, 0) is calculated by using pixels (1, 3) and (1, 1) for the y-gradient:
Ry = 255 − 255 = 0,
yielding Δy2 = 02 + 1022 + 02 = 10404.
Gy = 255 − 153 = 102,
By = 153 − 153 = 0,
Thus, the energy of borderpixel (1, 0) is 41616 + 10404 = 52020.
energyMatrix
The energy matrix is constructed by getting the energy at each pixel (x, y). For example, using the 3-by-4 image from the previous section, the energy matrix would be:
| 20808 | 52020 | 20808 |
| 20808 | 52225 | 21220 |
| 20809 | 52024 | 20809 |
| 20808 | 52225 | 21220 |
findVerticalSeam
The findVerticalSeam() method returns an array of length H such that entry i is the column number of the pixel to be removed from row i the image.
For example, consider [the 6-by-5 image](the 6-by-5 image) below:
| ( 78,209, 79) | ( 63,118,247) | ( 92,175, 95) | (243, 73,183) | (210,109,104) | (252,101,119) |
| (224,191,182) | (108, 89, 82) | ( 80,196,230) | (112,156,180) | (176,178,120) | (142,151,142) |
| (117,189,149) | (171,231,153) | (149,164,168) | (107,119, 71) | (120,105,138) | (163,174,196) |
| (163,222,132) | (187,117,183) | ( 92,145, 69) | (158,143, 79) | (220, 75,222) | (189, 73,214) |
| (211,120,173) | (188,218,244) | (214,103, 68) | (163,166,246) | ( 79,125,246) | (211,201, 98) |
The corresponding pixel energies are shown below, with a minimum energy vertical seam highlighted in pink.
In this case, findVerticalSeam() returns the array { 3, 4, 3, 2, 2 }.
| 57685 | 50893 | 91370 | 25418 | 33055 | 37246 |
| 15421 | 56334 | 22808 | 54796 | 11641 | 25496 |
| 12344 | 19236 | 52030 | 17708 | 44735 | 20663 |
| 17074 | 23678 | 30279 | 80663 | 37831 | 45595 |
| 32337 | 30796 | 4909 | 73334 | 40613 | 36556 |
Remember that seams cannot wrap around the image. When there are multiple vertical seams with minimal total energy, your method should return the leftmost seam (based on its starting position on the top row).
The behavior of findHorizontalSeam() is analogous to that of findVerticalSeam() except that it returns an array of length W such that entry j is the row number of the pixel to be removed from column j of the image.
removeVerticalSeam
This removeVerticalSeam method replaces this.picture with a new Picture object and decreases this.width by 1.
The new picture is a copy of the old picture with the seam pixels removed.
The removeHorizontalSeam method is analogous, except that it decreases this.height by 1.
Notice that copying the picture is necessary, because you cannot change the picture’s width or height. And there is no method to copy the image; you will need to copy each pixel one at a time in this method.
removeHoriztonalSeam
See mention above
Validating Seams
Both of the seam removal methods need to handle edge conditions. They should throw an exception when called with invalid arguments:
- Throw a
NullPointerExceptionif eitherremoveVerticalSeam()orremoveHorizontalSeam()is called with a null argument. - Throw an
IllegalArgumentExceptionif eitherremoveVerticalSeam()orremoveHorizontalSeam()is called with an array of the wrong length or if the array is not a valid seam (either an entry is outside the height/width bounds or two adjacent entries differ by more than 1). - Throw an
IllegalArgumentExceptionif eitherremoveVerticalSeam()orremoveHorizontalSeam()is called when the width or height of the current picture is 1, respectively.
Grading
Note: Your code must pass checkstyle before you can get any points for it on this assignment.
To help prepare you for implementing this project, please review the specifications and ask questions. Prior to writing the code for this project, check your understanding of the specifications via the P2 Readiness Quiz in gradescope.
| Project Part | Weight |
|---|---|
| Readiness Quiz (via gradscope assignment) | 30% |
| Correctness (via autograder) | 50% |
| Code Review | 20% |