Maximum Likelihood Learning and Logistic Regression

Review: Linear Regression

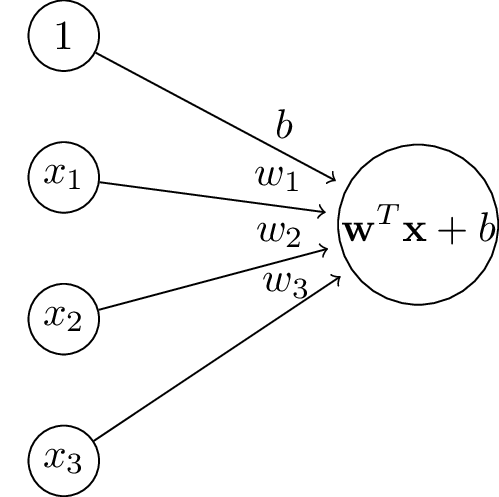
A single-layer network: inputs x1 through x3 and a bias input of 1 feed weights into a summation unit that computes w^T x + b.

The goal was to find weight values to minimize MSE on some training data: fitting a hyperplane.

Turning our single layer network into a probability distribution...

  • This is the logistic or sigmoid function:

    σ(z)=ez1+ez=11+e−z\sigma(z) = \frac{e^z}{1 + e^{z}} = \frac{1}{1 + e^{-z}}

  • It looks like this:

Today: Logistic Regression

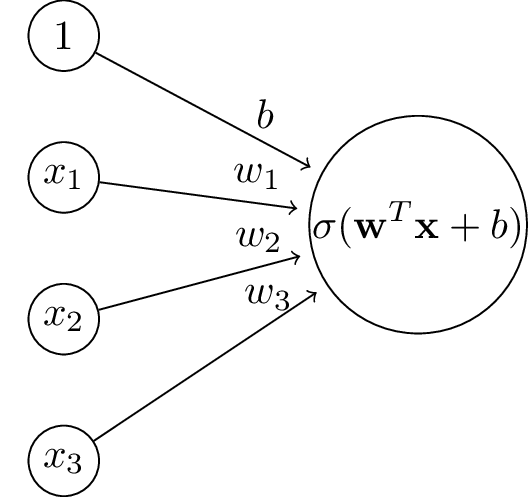
After applying a sigmoid non-linearity we can interpret the output as a probability.

  • If we let z=wTx+bz = \mathbf{w}^T\mathbf{x} + b, we end up with:

    P(y=1∣x,w)=σ(wTx+b)=11+e−(wTx+b)P(y=0∣x,w)=1−σ(wTx+b)\begin{split} P(y = 1 \mid \mathbf{x}, \mathbf{w}) &= \sigma( \mathbf{w}^T\mathbf{x} + b ) = \frac{1}{1 + e^{-(\mathbf{w}^T\mathbf{x }+ b)}}\\ P(y = 0 \mid \mathbf{x}, \mathbf{w}) &= 1 - \sigma( \mathbf{w}^T\mathbf{x} + b ) \end{split}

Squashing a Line

  • z=wx+bz = wx + b is a line
  • σ\sigma squashes it into (0,1)(0, 1)
  • Big ww: a sharp step
  • Small ww: a gradual ramp
  • bb slides it left and right
  • σ(z)≥0.5\sigma(z) \geq 0.5 exactly when z≥0z \geq 0: that is the decision boundary

Training...

  • Left: the model. Right: its cost for every setting of (b,w)(b, w)
  • Each gradient descent step moves the point downhill, and the curve follows
  • No setting fits every point: the cost never reaches 0

Two Inputs: A Squashed Plane

  • σ(w1x1+w2x2+b)\sigma(w_1 x_1 + w_2 x_2 + b): a plane, squashed
  • Training tilts and sharpens it to fit the labels
  • From above: predict 1 where P(y=1)≥0.5P(y = 1) \geq 0.5
  • The boundary w1x1+w2x2+b=0w_1 x_1 + w_2 x_2 + b = 0 is a straight line. No line separates these classes perfectly.

Aside: Derivative of the Sigmoid/Logistic Function

The logistic function has a simple derivative:

σ′(x)=σ(x)(1−σ(x))\sigma'(x) = \sigma(x)(1 - \sigma(x))

The logistic function and its derivative, a bump that peaks at 0.25 at zero.

Maximum a Posteriori Learning

  • Goal is to learn the parameters θ\theta of a probabilistic model.

  • One option is to attempt to find the single most probable set of parameters given our data and our prior:

    θMAP=argmaxθP(D∣θ)P(θ)\theta_{MAP} = \text{argmax}_\theta P(\mathcal{D} \mid \theta) P(\theta)

  • Laplace smoothing for naive Bayes can be seen as an example of this!

Maximum Likelihood Learning

  • An even simpler alternative is to just pick the parameters that make the data most probable:

    θML=argmaxθP(D∣θ)\theta_{ML} = \text{argmax}_\theta P(\mathcal{D} \mid \theta)

  • P(D∣θ)P(\mathcal{D} \mid \theta) is commonly referred to as likelihood:

    L(θ)=P(D∣θ)=∏xi∈DP(xi∣θ)\mathcal{L}(\theta) = P(\mathcal{D} \mid \theta) = \prod_{\mathbf{x}_i \in \mathcal{D}} P(\mathbf{x}_i \mid \theta)

    (For any one setting of θ\theta, the likelihood is the probability of the data we actually saw: a measure of how probable (likely) that data is given those parameters. But as a function of θ\theta it is not a probability distribution: it doesn't have to sum to 1 across settings of θ\theta.)

  • Simple example... Let's say θ\theta represents the probability that a rigged coin will come up heads: θ=.9\theta = .9. What is the likelihood of observing the following outcomes?

    [Heads,  Tails,  Heads][Heads,\; Tails,\; Heads]

  • What value of θ\theta would maximize the likelihood for this data set?

  • Numerically, we are usually better off working with the log likelihood:

    LL(θ)=∑xi∈Dlog⁡P(xi∣θ)\mathcal{LL}(\theta) = \sum_{\mathbf{x}_i \in \mathcal{D}} \log P(\mathbf{x}_i \mid \theta)

One Weird Trick...

  • We want a likelihood function for our binary classifier. It could look like this:

    L(w)=∏i=1n{P(y=1∣xi,w),if yi=1P(y=0∣xi,w),if yi=0\mathcal{L}(\mathbf{w}) = \prod_{i=1}^n \begin{cases} P(y = 1 \mid \mathbf{x_i}, \mathbf{w}), \text{if } y_i = 1 \\ P(y = 0 \mid \mathbf{x_i}, \mathbf{w}), \text{if } y_i = 0 \\ \end{cases}

  • This is much nicer to work with:

    L(w)=∏i=1nP(y=1∣xi,w)yi×P(y=0∣xi,w)1−yi\mathcal{L}(\mathbf{w}) = \prod_{i=1}^n P(y = 1 \mid \mathbf{x_i}, \mathbf{w})^{y_i} \times P(y = 0 \mid \mathbf{x_i}, \mathbf{w})^{1-y_i}

    (remember... a1=a,a0=1a^1 = a, a^0 = 1)

  • This makes the log likelihood:

    LL(w)=∑i=1n[yilog⁡P(y=1∣xi,w)+(1−yi)log⁡P(y=0∣xi,w)]\mathcal{LL}(\mathbf{w}) = \sum_{i=1}^n \Big[ y_i \log P(y = 1 \mid \mathbf{x_i}, \mathbf{w}) + (1 - y_i) \log P(y = 0 \mid \mathbf{x_i}, \mathbf{w}) \Big]

    (remember... log⁡b(xy)=ylog⁡b(x)\log_b(x^y) = y\log_b(x))

  • The goal is to maximize the log likelihood, which is the same as minimizing the negative log likelihood:

    −LL(w)=−∑i=1n[yilog⁡P(y=1∣xi,w)+(1−yi)log⁡P(y=0∣xi,w)]-\mathcal{LL}(\mathbf{w}) = -\sum_{i=1}^n \Big[ y_i \log P(y = 1 \mid \mathbf{x_i}, \mathbf{w}) + (1 - y_i) \log P(y = 0 \mid \mathbf{x_i}, \mathbf{w}) \Big]

Maximum Likelihood for Logistic Regression:

  • This loss function is usually called cross-entropy.

    −LL(w)=−∑i=1n[yilog⁡(σ(wTxi+b))+(1−yi)log⁡(1−σ(wTxi+b))]-\mathcal{LL}(\mathbf{w}) = -\sum_{i=1}^n \Big[ y_i \log(\sigma( \mathbf{w}^T\mathbf{x}_i + b )) + (1 - y_i) \log (1 - \sigma( \mathbf{w}^T\mathbf{x}_i + b )) \Big]

  • Quiz: What is the cross-entropy loss for σ(wTxi+b)=1\sigma( \mathbf{w}^T\mathbf{x}_i + b ) = 1 and yi=0y_i = 0? yi=1y_i = 1?

    Remember... log⁡(1)=0,   log⁡(0)=−∞\log(1) = 0, ~~~ \log(0) = -\infty

Why not just use MSE?

  • Zero and one are numbers, so there is no reason we couldn't use the loss function we used for linear regression:

    E(w)=∑i=1n(yi−σ(wTxi+b))2E(\mathbf{w}) = \sum_{i=1}^n (y_i - \sigma(\mathbf{w}^T\mathbf{x}_i + b))^2

  • Here is how the two loss functions compare:

The Gradient Looks Familiar

  • Using σ′=σ(1−σ)\sigma' = \sigma(1 - \sigma), the cross-entropy's partial derivatives come out to

    ∂(−LL)∂wj=∑i=1n(σ(wTxi+b)−yi) xi,j∂(−LL)∂b=∑i=1n(σ(wTxi+b)−yi) \frac{\partial (-\mathcal{LL})}{\partial w_j} = \sum_{i=1}^n \big(\sigma(\mathbf{w}^T\mathbf{x}_i + b) - y_i\big)\, x_{i,j} \qquad \frac{\partial (-\mathcal{LL})}{\partial b} = \sum_{i=1}^n \big(\sigma(\mathbf{w}^T\mathbf{x}_i + b) - y_i\big)

  • So the gradient descent updates are

    w←w+η∑i=1n(yi−σ(wTxi+b)) xib←b+η∑i=1n(yi−σ(wTxi+b))\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} + \eta \sum_{i=1}^n \big(y_i - \sigma(\mathbf{w}^T\mathbf{x}_i + b)\big)\, \mathbf{x}_i \\ b &\leftarrow b + \eta \sum_{i=1}^n \big(y_i - \sigma(\mathbf{w}^T\mathbf{x}_i + b)\big) \end{aligned}

  • Exactly the linear regression update, with the prediction run through σ\sigma: error times input

Minimizing Cross Entropy Loss for Logistic Regression

  • Unlike linear regression, finding the minima for logistic regression does not have a closed-form solution.
  • We can use simple gradient descent, but it is more common to use specialized solvers that calculate or approximate the Hessian (multi-dimensional generalization of the second derivative).
  • The loss function for logistic regression is convex: there are no local minima to get stuck in. (One exception: if the classes are perfectly separable there is no minimum at all; the weights grow without bound unless we regularize.)

Regularization

  • We can add a penalty to the loss that discourages large weights:

    −LL(w,b)+λ∥w∥2where∥w∥2=∑jwj2-\mathcal{LL}(\mathbf{w}, b) + \lambda \|\mathbf{w}\|^2 \qquad \text{where} \qquad \|\mathbf{w}\|^2 = \sum_{j} w_j^2

  • λ\lambda is a hyperparameter: bigger λ\lambda means smaller weights, a flatter sigmoid, and less confident predictions

  • Fixes the separable-data problem, and helps with overfitting in high-dimensional settings

  • Scikit-learn's LogisticRegression regularizes by default. Its C works the other way: bigger C means less regularization.

What If We Have More Than Two Classes?

Pros and Cons of Logistic Regression

  • Pros:
    • Simple and explainable: individual attribute coefficients indicate the relationship between the attribute and the class. Let's look at an example...
    • No local minima means that we can be confident that when our algorithm converges we have the "correct" model.
    • Prediction is fast.
    • Provides a real-valued score function that may be interpreted as a probability.
    • Looking ahead: provides key machinery for multi-layer neural networks.
  • Cons
    • Linear decision boundary

Interactive figures are drawn by lr_demos.js; the static figures come from logistic.py (the .svg files) and figs/*.tex (the network diagrams). Build with marp --html logistic_regression.md --html is required: the demos are inline <div>s plus a <script>. Bullets written with "*" unfold one at a time, and on demo slides each reveal also advances the animation, so the clicker drives everything. Mouse interaction (dragging, sliders, buttons) is extra and only affects the window you use it in. The three demos replace the animations from the "Animations of Logistic Regression with Python" article, which is now a 404. The previous (pandoc) version of this deck is logistic_regression_old.md.

This is the picture I drew on the board in the recorded lecture. Each click moves w and b; the sliders are for questions. The red triangles are the 1s and the blue circles the 0s; they are the training data for the next slide. Without b the line has to go through the origin, so the sigmoid would always be centred at x = 0. b is a weight attached to a constant input of 1, not a hyperparameter. A negative w flips the curve: the slider goes there if anyone asks.

The orange dot on the right IS the orange curve on the left. The thin lines run from each point to the model's prediction: their length is |y - p|. The cross-entropy charges -log(1 - length) for each one, so a long line costs far more than a short one. The gray curve is where we started: shifted to the left, so it says 1 for most of the points. "Cost" is the mean cross-entropy, which we derive in a few slides. We could use MSE here instead; the question of which loss is right is the second half of today. Note the long curved valley: w and b trade off against each other because the x values are not centred. 120 iterations, eta = 0.8. Click the contour plot to start somewhere else.

Step 1 runs 60 iterations of batch gradient descent from w = 0, b = 0, where the surface is flat at 0.5. Step 2 rotates to straight overhead. It gets 27 of the 32 training points right. The thin vertical lines are each point's error, |y - p|, as on the previous slide. The plot under the bullets is the cost (mean cross-entropy) over (w1, w2), with b held at its trained value (-0.73), so we can draw it: the real surface has three parameters. The descent path (whose b is changing too) ends at the minimum, cost 0.368, not 0.

# Bayesian Learning * In Bayesian learning, we use data to update a probability distribution over our model parameters $\theta$ given our training data $\mathcal{D} = (\mathbf{x}_1, \mathbf{x}_2, ... \mathbf{x}_n)$: * $P(\theta \mid \mathcal{D}) = \frac{ P( \mathcal{D} \mid \theta) P(\theta)} {P(\mathcal{D})}$ * The goal here is *not* to find the single best fit (or **point estimate**) for our parameters. Instead, we maintain a probability distribution over our parameters. * This is related to the idea of ensemble learning. * Here is a recent survey if you are interested: [Hands-on Bayesian Neural Networks - a Tutorial for Deep Learning Users](https://arxiv.org/abs/2007.06823)

Answers: 0.9 x 0.1 x 0.9 = 0.081. The maximum is at theta = 2/3, the fraction of heads: (2/3)(1/3)(2/3) = 4/27, about 0.148. (In the recorded lecture I said "four ninths"; it is 4/27.)

Added brackets: without them the minus sign (and the sum) applies only to the first term.

Derivation, per point, with p = sigma(z): d/dz [-y log p - (1 - y) log(1 - p)] = -y (1 - p) + (1 - y) p = p - y. Then dz/dw_j = x_j. Compare the last slide of the gradient descent lecture.

The old version of this slide said the loss is "guaranteed to have a single global minima." Convexity rules out local minima, but on separable data the minimum does not exist: Exercise 3 of the lab. The animations link on the old slide is a 404; the demos earlier in the deck replace it.

Teaser only; more later in the semester. Scikit-learn minimizes (1/2)||w||^2 + C * sum of the per-point losses, so C is roughly 1/(2 lambda). The bias b is not penalized. Lab Exercise 3 shows the separable case: as C grows, ||w|| keeps growing.

The example is titanic.py (standardized features, no penalty): about 84% correct on the test set; Sex (1 = male) -1.21 and Pclass -0.95 are the biggest weights.