Linear Probing

• Problem: primary clustering - collisions tend to cause clusters of occupied buckets.
• The larger the cluster gets, the higher the probabilility that it will grow.

Impact of Load Factor on Cost

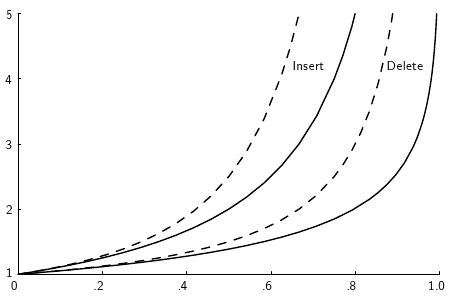
Load factor is on the x-axis, expected number of buckets accessed on the y-axis.

(From OpenDSA Data Structures and Algorithms book)

Solution #1: Quadratic Probing

• Probe function: \(p(K, i) = c_1 \times i + c_2 \times i^2\)
• Bucket to access: \(h(K) + p(K, i)\), where:
  • \(K\) - original key
  • \(h(K)\) - result of hashing the key
  • \(p(K, i)\) - offset from the original hash location to check after \(i\) collisions
• For example, assuming \(c_1 = 1, c_2 = 1\):
  • After one collision: \(p(K, 1) = 1 + 1 = 2\)
  • After two collisions: \(p(K, 2) = 2 + 4 = 6\)
  • After one collision: \(p(K, 3) = 3 + 9 = 12\)
  • After one collision: \(p(K, 4) = 4 + 16 = 20\)
• Problem:
  • Secondary Clustering: Keys that hash to the same bucket will follow the same probe sequence.

Solution #2: Double Hashing

• Probe function: \(p(K, i) = h_2(K) \times i\)
• Example with \(h_2(K) = 1 + K \% 7\)
  • After one collision for \(K=11\): \(p(K, 1) = 5 \times 1 = 5\)
  • After two collisions for \(K=11\): \(p(K, 2) = 5 \times 2 = 10\)
  • After two collisions for \(K=11\): \(p(K, 3) = 5 \times 3 = 15\)
• Different keys follow different probe sequences, so this is resistant to both primary and secondary clustering.

Problems/Challenges with Hashing

• No ordered iteration.
• Iteration can be relatively inefficient when it involves iterating past empty buckets.
• Good hashing can lead to poor cache performance.
• Worst case performance is very bad.

What Gets used In The Wild?

C#/.net Dictionary

• Prime-number-sized tables
• Collision Resolution: Separate Chaining (in an array)

• Max load factor: 1.0

  source

  blog post

Python 2

• Closed hashing
• Power-of-two table sizes
• Hash function: grab lower order bits (no effort to avoid collisions)

  • Calculating mask:

    mp->ma_mask = newsize - 1;

  • Finding index:

    i = hash & mask;

• Collision resolution: fancy double hashing

  • Original hash \(j\) is modified according to:

    perturb >>= PERTURB_SHIFT;
    j = (5*j) + 1 + perturb;

  • perturb is initialized to the original hash, then bit-shifted after every collision.

  • Default load factor .66

Implementation in: Python-2.7.2/Objects/dictobject.c. Source can be downloaded from www.python.org.

Python 3.6+

Update in Python 3:

the dictionary:

    d = {'timmy': 'red', 'barry': 'green', 'guido': 'blue'}

is currently stored as:

    entries = [['--', '--', '--'],
               [-8522787127447073495, 'barry', 'green'],
               ['--', '--', '--'],
               ['--', '--', '--'],
               ['--', '--', '--'],
               [-9092791511155847987, 'timmy', 'red'],
               ['--', '--', '--'],
               [-6480567542315338377, 'guido', 'blue']]

Instead, the data should be organized as follows:

    indices =  [None, 1, None, None, None, 0, None, 2]
    entries =  [[-9092791511155847987, 'timmy', 'red'],
                [-8522787127447073495, 'barry', 'green'],
                [-6480567542315338377, 'guido', 'blue']]

Only the data layout needs to change.  The hash table
algorithms would stay the same.

descripion: https://mail.python.org/pipermail/python-dev/2012-December/123028.html

source: https://github.com/python/cpython/blob/main/Objects/dictobject.c

Ruby

• Originally:
  • Prime-number-sized tables
  • Collision resolution: chaining
  • Max load factor: 5
• More recently:
  • Very similar to the Python3 approach

Original source: https://github.com/ruby/ruby/blob/ruby_2_3/st.c Updated source: https://github.com/ruby/ruby/blob/ruby_3_0/st.c

Java 7 (We’ve seen…)

• Power-of-two table sizes
• Hash Function: bit scrambling, then use lower-order bits.
• Collision resolution: Chaining
• Default load factor: .75

static int hash(int h) {
        // This function ensures that hashCodes that differ only by
        // constant multiples at each bit position have a bounded
        // number of collisions (approximately 8 at default load factor).
        h ^= (h >>> 20) ^ (h >>> 12);
        return h ^ (h >>> 7) ^ (h >>> 4);
    }


    /**
     * Returns index for hash code h.
     */

    static int indexFor(int h, int length) {
        return h & (length-1);
    }

source (GPL V2.0)

Java 8+

• Power-of-two table sizes
• Hash Function: a little bit shifting, then use lower-order bits.
• Collision resolution: Chaining, CONVERT TO TREES IF THE CHAIN GETS LONGER THAN 8!
• Default load factor: .75

static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Java 16 Source: https://github.com/openjdk/jdk/blob/jdk-16+36/src/java.base/share/classes/java/util/HashMap.java