Data Structures And Algorithms: PA #4

James Madison University, Spring 2013

Programming Assignment #4: Sorting

Introduction

Quick sort is the fastest known comparison-based sorting algorithm when applied to large, unordered, sequences. It also has the advantage of being an in-place (or nearly in-place) sort. Unfortunately, quick sort has some serious failings: it's worst-case performance is O(n²), and it is not stable. Merge sort shares neither of these disadvantages: it is stable and it requires O(n log n) steps in the worst case. Unfortunately, merge sort requires O(n) additional space and it runs significantly more slowly than quick sort on most inputs.

What we really want is a sorting algorithm that is as fast as quick sort, stable, in-place, with O(n log n) worst-case performance. Sadly, no such algorithm has yet been discovered. In practice, most code libraries follow one of two paths: either they provide a modified version of quick sort that is able to avoid worst-case behavior on typical inputs, or they provide a modified version of merge sort that is able to close some of the performance gap through careful optimizations. The second approach has recently become popular. Both Python (starting in version 2.3) and Java (starting in version 7) use timsort as their default sorting algorithm. Timsort is a modified version of merge sort that includes several enhancements: it uses a more space-efficient merge operation, it takes advantage of partially sorted arrays by finding and merging exiting sorted regions, and it uses a non-recursive binary insertion sort to handle short unsorted regions.

The objective of this assignment is to write a modified version of merge sort that exhibits better performance than the standard version described in our textbook. You won't use all of the tricks from timsort -- the Python implementation of timsort requires more than 1,000 lines of C code. Instead you will implement two key improvements that should significantly improve performance without requiring a great deal of additional code. You will also write timing code that will allow you to experimentally evaluate the impact of your improvements.

Improvement One: Switching Strategies

The first improvement is based on the observation that merge sort is actually slower than simple O(n²) sorts for small input sizes. This may seem surprising given that merge sort is an O(n lg n) sorting algorithm. However, it is important to keep in mind that big-O analysis is only concerned with rates of growth. 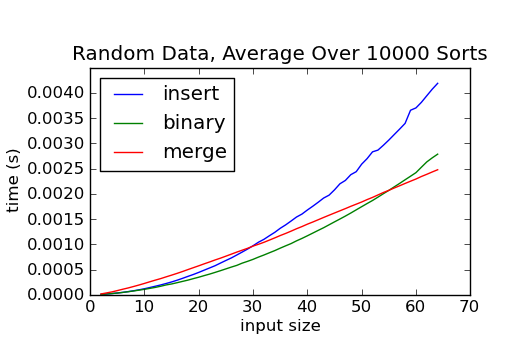An O(n lg n) algorithm will always be faster than an O(n²) algorithm eventually, but that doesn't mean the O(n²) algorithm can't be faster for small inputs. The following figure was created by timing merge sort, insertion sort, and binary insertion sort on small randomly ordered lists from size 2 to size 64: .

As you can see, binary insertion sort is the fastest of the three algorithms until around n = 55. At that point, merge sort becomes faster and it remains faster for all larger inputs.

A a reminder, the following pseudocode describes the overall logic of the merge sort Algorithm:

mergeSort(sub-list)
    If sub-list is has more than one entry: 
        Recursively mergeSort the left half
        Recursively mergeSort the right half
        Merge the two sorted halves.

This logic recursively splits the original list into smaller and smaller sub-lists until the recursion bottoms out at lists of size one. This means that every time a large list is sorted, there are many recursive calls to merge sort that have small input sizes. In light of the figure above, that approach doesn't make much sense: merge sort is not a competitive sorting algorithm on small inputs. It would make more sense to recursively break the input into smaller and smaller pieces until some threshold is reached, and then switch strategies to a sorting algorithm that is more efficient on those small inputs.

The following pseudocode describes this alternate approach:

mergeSort(sub-list)
    If sub-list is has fewer than THRESHOLD entries:
        Sort the sub-list with binary insertion sort. 
    Otherwise: 
        Recursively mergeSort the left half
        Recursively mergeSort the right half
        Merge the two sorted halves.

Choosing an appropriate value for THRESHOLD requires some experimentation. One of the requirements of this assignment is that you select an appropriate threshold value and provide data to justify your choice.

Improvement Two: Efficient Merges

The merge algorithm we discussed in class consists of the following three stages:

Create a new list large enough to contain both sub-lists that are being merged.
Merge the values from the two sub-lists into the newly created list.
Copy the values from the new list back into the original list.

If n is the combined size of the two sub-lists being merged, this algorithm allocates a list of size n in stage 1, and requires n assignment operations in stage 3. The following alternative approach cuts both of those values from n to around n/2:

Create a new list just large enough to hold the values from the first sub-list.
Copy the values from the first sub-list to the newly created list
Merge the values from newly created list and the right sub-list into the original list.

Here are some ASCII graphics illustrating the process:

Original sorted sub-lists:

      ________________________________________
     | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------
 start-^           mid-^               end-^

Allocate new space:

      ___________________
     |   |   |   |   |   |
      -------------------

      ________________________________________
     | 1 | 3 | 5 | 7 | 9 | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------
 start-^           mid-^               end-^

Copy the first sub-list into the newly allocated space:

      ___________________
     | 1 | 3 | 5 | 7 | 9 |
      -------------------

      ________________________________________
     |   |   |   |   |   | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------

Initialize a to be the index of the first position in the new list, b to be the index of the first position of the right sub-list, and next to be the next available position for merging:

      ___________________
     | 1 | 3 | 5 | 7 | 9 |
      -------------------
     a-^
      ________________________________________
     |   |   |   |   |   | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------
  next-^                 b-^

First step of merge:
Since new[a] < list[b], new[a] is copied to list[next].
a and next are incremented.

      ___________________
     | 1 | 3 | 5 | 7 | 9 |
      -------------------
         a-^
      ________________________________________
     | 1 |   |   |   |   | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------
      next-^             b-^

Since list[b] < new[a], list[b] is copied to list[next].
b and next are incremented.

      ___________________
     | 1 | 3 | 5 | 7 | 9 |
      -------------------
         a-^
      ________________________________________
     | 1 | 2 |   |   |   | 2 | 4 | 6 | 8 | 10 |
      ----------------------------------------
          next-^             b-^

Continue Merging until complete:

      ___________________
     | 1 | 3 | 5 | 7 | 9 |
      -------------------

      ________________________________________
     | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
      ----------------------------------------

Requirements

You should use the python modules sorts.py and time_sorts.py as a starting point. You must supplement the completed sorting algorithms provided in sorts.py with three additional algorithms:

mergeSort1 - This should be a modified version of merge sort that switches strategies on small inputs, as described above.
mergeSort2 - This should be a modified version of merge sort that uses the optimized merging strategy described above.
mergeSort3 - This should be a modified version of merge sort that incorporates both of the improvements described above.

You must also modify time_sorts.py so that it prints out timing information for each of the sorting algorithms in sorts.py, including the modified merge sort algorithms that you develop. All algorithms should be timed on both random and ordered input lists with sizes ranging from 200 to 2000 elements. The O(n lg n) sorts should also be timed on random inputs with sizes ranging from 20,000 to 200,000 elements. All timings should be averaged across 10 sorts.

The following output illustrates the correct format for the printed results:

----------Random Lists Averaged Over 10 Sorts----------
                 200       400       600       800      1000      1200      1400      1600      1800      2000
Selection    0.00189   0.00454   0.00984   0.01550   0.02402   0.03554   0.04733   0.06110   0.08097   0.09830
Insertion    0.00128   0.00580   0.01295   0.02406   0.03789   0.05293   0.07699   0.09701   0.12730   0.15797
Binary       0.00120   0.00418   0.00989   0.01707   0.02601   0.03809   0.05392   0.06789   0.08522   0.10496
QuickSort    0.00025   0.00053   0.00083   0.00120   0.00156   0.00181   0.00220   0.00269   0.00311   0.00328
MergeSort    0.00054   0.00115   0.00182   0.00254   0.00344   0.00423   0.00494   0.00581   0.00615   0.00686
MergeSort1   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort2   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort3   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000

----------Ordered Lists Averaged Over 10 Sorts----------
                 200       400       600       800      1000      1200      1400      1600      1800      2000
Selection    0.00131   0.00455   0.00952   0.01608   0.02404   0.03415   0.04698   0.06007   0.07686   0.09421
Insertion    0.00004   0.00006   0.00008   0.00010   0.00013   0.00015   0.00018   0.00021   0.00023   0.00026
Binary       0.00021   0.00043   0.00074   0.00103   0.00129   0.00164   0.00212   0.00237   0.00276   0.00297
QuickSort    0.00153   0.00526   0.01233   0.02164   0.03264   0.04593   0.06391   0.08260   0.10496   0.12799
MergeSort    0.00053   0.00109   0.00172   0.00238   0.00307   0.00394   0.00447   0.00514   0.00595   0.00687
MergeSort1   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort2   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort3   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000

----------Random Lists Averaged Over 10 Sorts----------
               20000     40000     60000     80000    100000    120000    140000    160000    180000    200000
QuickSort    0.04365   0.09904   0.14485   0.19953   0.25359   0.31092   0.36378   0.44178   0.49209   0.54231
MergeSort    0.08707   0.18716   0.28868   0.39504   0.50289   0.60858   0.72009   0.83640   0.95140   1.05808
MergeSort1   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort2   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000
MergeSort3   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000   0.00000

Your output should exactly match the format above: times should be displayed in seconds with five decimal places of precision. Each column should be labeled with the corresponding list size, etc.

Along with your modified Python modules you must also submit a .txt files that contains the output of your program on a sample execution. That file should also contain a description of the approach that you used to selecting an appropriate threshold value for switching sorting strategies in mergeSort1 and mergeSort3, along with the data that you used in making your decision.

Hints

Keep in mind that your new sorting algorithms need to be correct as well as efficient. One way to test your code is to compare its output to Python's built in sort method. For example:

>>> a = [random.randint(0, 500) for _ in range(500)] # Generate a random list.
>>> b = a[:]                                         # Copy the list. 
>>> b.sort()                                         # Sort the copy.
>>> sorts.insertionSort(a)                           # Sort using my sort.
>>> a == b                                           # Compare results.  
True

Given the figure above, you may be tempted to select 55 as the threshold for switching sorting strategies. Since merge sort appears to be slower than binary insertion sort for all sizes below 55, it seems obvious that merge sorting at any smaller size will result in wasted time. What you should keep in mind is that the figure above shows the running time for merge sort if it continues to recce's all the way down to lists of size one. The choice is not between switching to binary insertion sort or running merge sort all the way to lists of size one, it is between switching strategies immediately or performing some additional splits, then switching strategies.
Implementing mergeSort1 and mergeSort3 will require you to complete a modified version of binaryInsertionSort that works on sub-lists.
Producing the table of results requires some fairly complex string formatting. You need to display the required number of decimal places and you need to ensure that the columns line up correctly. The recommended way to handle this sort of thing in Python is to use the format method of the string class. In its simplest form, format makes it possible to insert values into arbitrary strings. For example, the following statement inserts the values 1/3 and 2/3 into the indicated string:
```
>>> "A {0} B {1}".format(1./3, 2./3)
'A 0.333333333333 B 0.666666666667'
```
The first argument is converted to a string and inserted in place of {0} and the second is inserted in place of {1}.

The format method also makes it possible to control the way that inserted values are displayed. For example, we can limit the number of decimal places as follows:
```
>>> "A {0:.1f} B {1:.1f}".format(1./3, 2./3)
'A 0.3 B 0.7'
```
Here .1f indicates that the values should be displayed as floats, and that only one decimal place should be retained. More generally, the information after the colon is referred to as a format specifier. The syntax for format specifiers is governed by the Format Specification Mini-Language.
Format specifiers may also include a width value. The following ensures that both inserted fields will be at least 20 characters wide:
```
>>> "A {0:20.1f} B {1:20.1f}".format(1./3, 2./3)
'A                  0.3 B                  0.7'
```
This just scratches the surface of string formatting possibilities. I encourage you to read over the Python documentation for details and examples.

Handing In

You should submit two .py files and a .txt file through Blackboard before the deadline. As always, your code should conform to the CS240 Python Coding Conventions.

Acknowledgments

This assignment is based on a project originally developed by Dr. Chris Fox.