So far…

• Insertion sort \(\Theta(n^2)\) worst and average case.
• Selection sort \(\Theta(n^2)\) worst and average case.
• Is this good?

Merging…

Mergesort

  private static void mergesort(int[] items, int[] temp, 
                                int left, int right) {
    if (left == right) {
      return;
    }

    int mid = (left + right) / 2; 

    mergesort(items, temp, left, mid); 
    mergesort(items, temp, mid + 1, right); 

    merge(items, temp, left, mid, right);
  }

Socrative… Given that merge requires \(f(n)\) comparisons to merge \(n\) elements, provide a recurrence relation describing the worst-case number of comparisons performed by mergesort.

Merge

  private static void merge(int[] items, int[] temp, 
                            int left, int mid, int right) {

    for (int i = left; i <= right; i++) {
      temp[i] = items[i];// Copy subarray to temp
    }

    int i1 = left;
    int i2 = mid + 1;
    for (int curr = left; curr <= right; curr++) {
      if (i1 == mid + 1) { // Left subarray exhausted
        items[curr] = temp[i2++];
      } else if (i2 > right) { // Right subarray exhausted
        items[curr] = temp[i1++];
      } else if (temp[i1] <= temp[i2]) { // Get smaller value (COUNT THIS!)
        items[curr] = temp[i1++];
      } else {
        items[curr] = temp[i2++];
      }
    }
  }

Socrative… How many comparisons (between keys) are performed by merge in the worst case?

Mergesort Analysis

\(W(1) = 0\)

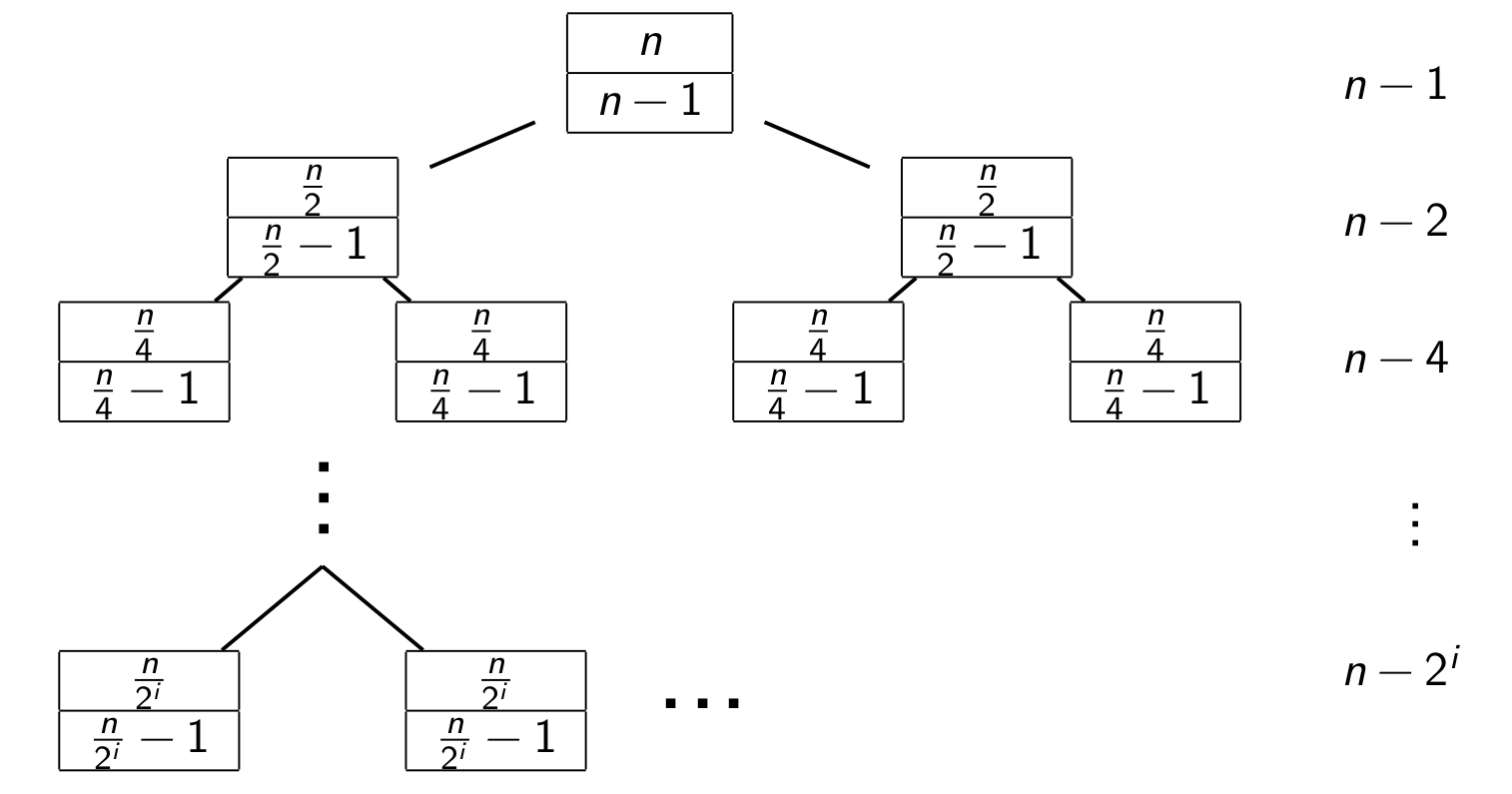
\(W(n) = n - 1 + 2W(\frac{n}{2})\)

Tree method…

Mergesort Analysis

Now we can write down the overall sum: \[\sum_{j=0}^i n - 2^j \]

\(i\) is determined by the initial condition…

\(n/2^i = 1\)

\(i = \log_2 n\)

Substituting: \(\sum_{j=0}^{\log_2 n} n - 2^j\)

Mergesort Analysis

Useful fact: \(\sum_{j=0}^{n} 2^j = 2^{n+1} - 1\)

\[\sum_{j=0}^{\log_2 n} n - 2^j \] \[ = \sum_{j=0}^{\log_2 n} n - \sum_{j=0}^{\log_2 n} 2^j \] \[ = n (\log_2 n + 1) - \sum_{j=0}^{\log_2 n} 2^j \] (Apply useful fact.) \[ = n (\log_2 n + 1) - (2^{\log_2 n + 1} - 1) \] \[ = n \log_2 n + n - (2n - 1)\] \[ = n \log_2 n - n + 1 \]

What about assignments?

Repeat the analysis for assignments…