Recursion Practice and Review

Your goal in this lab is to gain more experience solving computational programs with recursion. You will write recursive solutions for three programming challenges.

Collatz

The Collatz Conjecture is the claim that any integer greater than 1 will be reduced to 1 if you apply the following transformation: halve the number if it’s even, or triple the number and add 1 if it’s odd. Keep repeating the transformation on the resulting number until you arrive at 1.

The conjecture has not been proven true or false. However, it is true for all the numbers that have been tested. If you start at 10, the transformations lead to this sequence: 10 5 16 8 4 2 1. The Collatz count for 10 is 6, since it takes 6 steps to arrive at 1. If you start at 11, the transformations lead to this sequence: 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1. The Collatz count is 14.

Write class Collatz with a static method collatzCount. It accepts an int parameter for the number to transform. It returns the number of transformations needed to reach 1. If the number is already 1, the number of transformations is 0.

Solve this with recursion, not iteration.

Pascal

Pascal’s Triangle is a visualization of the coefficients of the expansion of \(~(x + y)^n~\). When \(~n~\) is 0, the expansion is \(~1~\). When \(~n~\) is 1, the expansion is \(~1x + 1y~\). When \(~n~\) is 2, the expansion is \(~1x^2 + 2xy + 1y^2~\). The coefficients for all values of \(~n~\) in [0, 6] are laid out in the rows of this truncated version of Pascal’s Triangle:

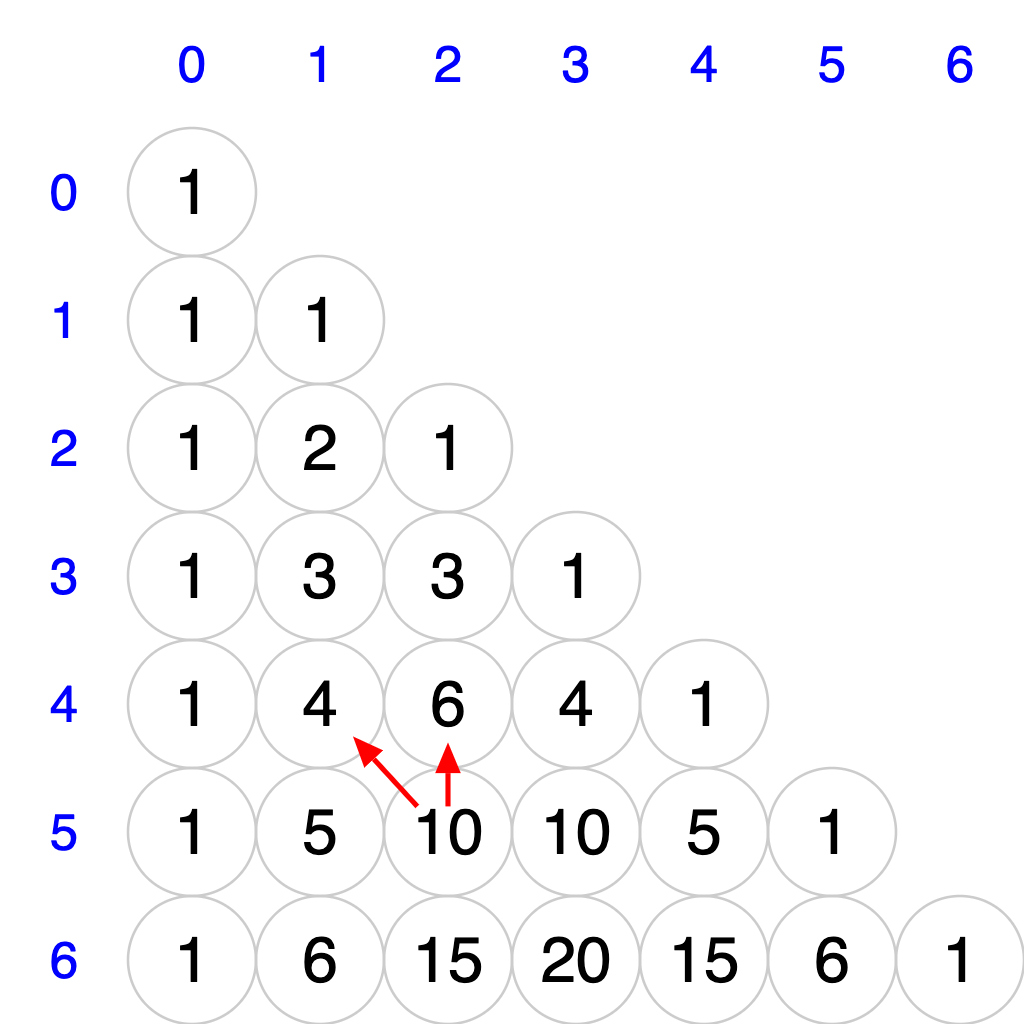
Create a class Pascal with a static recursive method pascal. It accepts a row and column of Pascal’s Triangle, both of type int, and it returns the coefficient at that row and column. The coefficient at a particular location is the sum of the coefficients to the north and northwest. Consider any value outside the triangle to be 0.

Solve this with recursion, not iteration.

Box

Suppose you have a colored box that contains other colored boxes. These other boxes may in turn contain colored boxes. The twice-nested boxes may contain more boxes still. And so on. You are looking for a box of a particular color, so you go looking through this mess.

Write class Box with this public interface:

• A constructor that accepts two parameters: a color name as a String and a List of its nested boxes.

• search – The search method must accept a single String parameter representing the color of the box to search for. It must return null if the a box with that color could not be found, or a LinkedList containing the sequence of box colors from the outermost box to a box of the appropriate color.

  Suppose you have this nesting structure:

  • red

    • yellow

      • pink

      • orange

      • blue

    • purple

      • mauve

      • cyan

  If you call search on the red box to find orange, you’ll get back the list [red, yellow, orange].

Solve this with recursion and just a little bit of iteration to visit the nested boxes within a particular level.

This main method builds the above hierarchy of boxes and searches for orange:

public static void main(String[] args) {
  Box pink = new Box("pink", List.of());
  Box orange = new Box("orange", List.of());
  Box blue = new Box("blue", List.of());
  Box mauve = new Box("mauve", List.of());
  Box cyan = new Box("cyan", List.of());
  Box purple = new Box("purple", List.of(mauve, cyan));
  Box yellow = new Box("yellow", List.of(pink, orange, blue));
  Box red = new Box("red", List.of(yellow, purple));

  System.out.println(red.search("orange"));
}

Going Further (Optional)

Just because a problem can be solved recursively, doesn’t mean it should be solved recursively. In most programming languages the overhead of making a method call is significantly higher than the cost of iterating in a loop. For each of the problems above, consider whether it would be reasonable to develop an iterative solution. If so, write and test the iterative solution (but do not submit it to Gradescope.)

• Collatz
• Pascal – Before working on this one, try running pascal(40, 20) using your recursive solution.
• Box

Submission

Your instructors are not providing the source code for JUnit tests in this lab. When your instructors provide tests, students often do not test code themselves and enter a frustrating game of trying to satisfy the grading machine. Please don’t do that. Test your code locally. Reason about its correctness. When you are reasonably confident in your solution, submit your code to Gradescope to run the autograder’s unit tests.

Acknowledgments

The original version of this lab was developed by Chris Johnson.