This is the multi-page printable view of this section. Click here to print.
Labs
1 - Uninformed Search Lab
Introduction
The goal of this lab is to implement and apply uninformed search algorithms and to become more familiar with Python. This lab was originally developed as part of the AI project at Berkeley University.
Resources
Useful API documents:
Files
The required files for this lab are provided in uninformedSearch.zip . The files you will need to modify are:
-
eightpuzzle.py (UNFINISHED) a representation of an eight piece sliding puzzle. You can directly run this file and watch your search problem solve an instance of the puzzle.
-
search.py (UNFINISHED) A set of uninformed search functions that operate on SearchProblem instances
Instructions
Download the zip file above and complete eightpuzzle.py and search.py
so that all functions conform to their Python docstrings. Test your completed
files by running
search_test.py
.
Storing States Efficiently
Graph search methods need to track visited states to avoid getting into infinite loops (and wasting computing time and space). You must utilize a python set object to store the visited/reached states. Hashing in Python (whether into a set or a dictionary) utilizes the __hash__ and __eq__ member functions of the object being stored.
Task: Augment the eightpuzzle.py to provide both the __hash__ and __eq__ functions
for the class EightPuzzleState. These are required for storing objects as keys in dictionaries
and sets.
Hint: To hash something, one approach could first turn the object into a String and then use the Python hash function (which knows how to change a String into a hashcode).
For the eq function, think about what makes two puzzles equal?
DFS and BFS Graph Search
Task: Augment the search.py and complete the breadthFirstSearchStats, depthFirstSearchStats,
and whateverFirstSearch functions so that they comply with their docstrings.
For the frontiers, a queue.LifoQueue object can be used as a stack and the queue.Queue object can serve as a queue. It is important that both types of frontiers share the same interface so that whateverFirstSearch does not need to distingish between them (they share the same member function names for most operations). The prototyped methods of depthFirstSearch and breadthFirstSearch must simply create the frontier and call whateverFirstSearch. They literally should be 2 lines of code each. Each method should return the tuple returned by whateverFirstSearch (see the docstring in whateverFirstSeach).
Frontier Mangement
All of your functions must add items to the frontier data structure in the order that the successors function returns the actions.
Until now (and based on what we have read), you may have thought of the frontier as just storing which state to visit next. But the goal of these methods is to construct PATHs from the start state to the goal state. In the assigned reading, a search tree is used to encode the path. To do this, as we remove items from the frontier, we need to know the parent state (so we know where to append this node in the tree). It is useful to think of this as a tree, but in Python, it is common to take another approach to this problem. Let each entry in the frontier be a tuple that consists of three items:
- the current state
- a list which represents the ordered actions required to move from the start state to the current state (in other words, the path from start to current)
- the cost of the actions taken from the root to the current node. You might think you could compute this as the length of the list - 1, however, some problems do not have uniform cost actions like the 8 piece puzzle. Notice that the
getSuccessorsfunction returns a tuple with the new state, the action taken, and the action cost. Your cost should be the running sum of the action costs.
For this lab, the “object” you push on the frontier must be a namedtuple. Tuples are similar to lists in Python except they are immutable. Using a namedtuple is nice and enables you to refer to items by name instead of just [0], [1], etc. We will briefly discuss in class what items to place in the tuple.
No additional Python imports
You may not add any imports to search.py or eightpuzzle.py. If you think
that you need to import a library, post a question to Piazza or email me.
Testing Your Code
If you have trouble with your submission, you may find it helpful to look at the unittests: search_test.py .
Fun Tests with Pacman
You can use your uninformed search methods to find a path to the nearest dot in Pacman.
The Pacman board will show an overlay of the states explored, and the order in which they were explored (brighter red means earlier exploration). Is the exploration order what you would have expected? Does Pacman actually go to all the explored squares on his way to the goal? Does either method find the most efficient path to the dot?
python pacman.py -l mediumMaze -p SearchAgent -a fn=dfs
python pacman.py -l mediumMaze -p SearchAgent -a fn=bfs
Hint: If Pacman moves too slowly for you, add the option --frameTime 0 (or some other value like 0.05 works well).
Rubric
| Item | Description | Points |
|---|---|---|
| BFS | Breadth-first graph search correct and passes test cases | 30 |
| DFS | Depth-first graph search correct and passes test cases | 30 |
| Hasheq | Implements __hash__ and __eq__ functions inside of eightpuzzle.py | 20 |
| Named tuple | whateverFirstSearch puts and retrieves namedtuples on the frontier | 15 |
| Style | Good coding style | 5 |
Submitting
Submit your completed version of eightpuzzle.py and search.py
through Gradescope. You have an unlimited
number of submissions. Note that the autograder is not verifying
your hasheq and namedtuple portions of the assignment.
Acknowledgements
I would like to thank the Berkeley AI team for developing the Pacman API and the scaffolding around this assignment.
2 - Informed Search Lab
Introduction
In this lab, you will write uniform cost search (UCS) and A* search methods in Python.
You will construct heuristics for A* specifcally for the eightpiece puzzle problem (the
two that were discussed in lecture).
This lab introduces priority queue objects in Python.
NOTE Technically UCS is an uninformed search method since it does not use knowledge about the goal location, but it is part of this lab so that we can compare how it performs against A*.
Resources
Useful API documents:
Files
Copy your Lab 1
files over to a new directory for this lab. You will need your search methods and the modified
eightpuzzle.py file with the hash functions added for this lab.
-
eightpuzzle.py (UNFINISHED) a representation of an eight piece sliding puzzle. You will add the two heuristic functions discussed in lecture.
-
search.py (UNFINISHED) A set of search functions that operate on SearchProblem instances. You will complete the UCS method by adapting whateverFirstSearch to work with this.
-
plot_search_performance.py (UNFINISHED) Python code to plot the results of your searchs on the 6 benchmark puzzles
Instructions
-
Copy the entire set of files from Lab 1
-
Complete the
aStarSearchStatsmethod withinsearch.pyso that it conforms to its Python docstring. NOTE: Completing theaStarSearchStatsmethod enablesuniformCostSearchStatsto use the call it and utilize thenullHeuristicfunction.
It is required that UCS be unchanged and that it just calls aStarSearchStats. You could change whateverFirstSearch to handle all 4 searches (although this is not a requirement). HINT: It is a good idea to use a namedtuple that stores f(x), g(x), and h(x) separately.
-
Complete the
tilesEightPuzzleHeuristicandmanhattenEightPuzzleHeuristicmethods inside ofeightpuzzle.py. These methods compute heuristics for the eight piece puzzle. The requirements of each method are detailed in their Python docstrings. When called directly, theeightpuzzle.pymodule will generate a random eight piece puzzle and use your code to solve it. As coded, it calls BFS, but you can change it to call UCS or A* so that you can test your code. -
Showcase the performance (expanded state count) between the different searches by creating a plot in python. This single plot needs to show the 6 puzzles on the X axis (the ones built by and used by
informed_search_test.py), the Y axis for each of these 6 points is the number of expand operations performed. You need to plot a line for each search: UCS, A* w/tiles, A* w/manhatten). An example of creating a plot with two lines is provided in the plot_search_performance.py .
Priority Queues in Python and Frontier Management
A* and UCS both required a priority queue. The priorityQueue object accepts a tuple (with any number of elements) and uses all the element in the tuple for creating the “key” that it will use for extracting the minimum value. For example, if all the first elements were distinct values, it would never need to access the other elements (which it would only use to break a tie). You might try storing a tuple with (f(x), node). However, since it is likely that more than 1 node in the priority queue will have the same f(x) value, which would require the priority queue to compare the second element in the tupe to break the tie, which is a node object. Since node is a namedtuple, it does not have a comparison method and thus, Python throws an error.
While several solutions exist for this situation, including adding comparative methods and or wrapping the item in a class as suggested in the PriorityQueue documentation. Here is a solution that works well in practice in Python. Given two elements on the priority queue with the same f(x), the A* algorithm does not care which one is extracted. Therefore, just store an extra element within the tuple stored on the priority queue, where the first element is f(x), the second element is some counter value (unique by construction), and then any remaining elements. Since each counter value is unique, it breaks all ties when the f(x) values are the same, and the elements that follow are never evaluated for key order.
In your A* method, you can create a counter at the beginning of
your function (count is imported from itertools):
from itertools import count
unique = count()
An example of adding a new item to the priority queue is:
pq.put((f(x), next(unique), node))
where node is a namedtupled that should contains 4 items:
- the state
- a list of actions to get from the start state to this state
- the cost so far so get to this state (g(x))
- the heuristical cost to get from this state to the goal (h(x))
While having items 3 and 4 (g(x) and h(x)) is redundant (since f(x) is already the first element), it greatly helps with debugging your code and is highly recommended.
Working with the EightPuzzle for heuristic computation
It may be helpful to have the puzzle in a 1d type structure (instead of the 2d array). You can use the following call to “flatten” the data into a 1d structure:
from itertools import chain
list(chain.from_iterable(state.cells))
Shorter Paths
Is it possible that a state/node appears in the priority queue more than once with A* search? If so, how do you handle this? Think about this question and the reached data structure used with graph search. The good news is that you can deal with this, but can you explain how your code will deal with this situation?
No additional Python imports
You may not add any imports to search.py or eightpuzzle.py. If you think
that you need to import a library, post a question to Piazza or email me.
Testing Your Code
If you have trouble with your submission, you may find it helpful to look at the unittests that are provided in the informed_search_test.py file.
Fun Tests with Pacman
You can use your informed search methods to find paths with different agents and cost functions in Pacman.
The Pacman board will show an overlay of the states explored, and the order in which they were explored (brighter red means earlier exploration). Is the exploration order what you would have expected? Does Pacman actually go to all the explored squares on his way to the goal? Does either method find the most efficient path to the dot?
python pacman.py -l bigMaze -z .5 --frameTime 0.04 -p SearchAgent -a fn=ucs
python pacman.py -l bigMaze -z .5 --frameTime 0.04 -p SearchAgent -a fn=astar,heuristic=manhattanHeuristic
Notice that the two paths have the same cost (they are both optimal). However the UCS should have expanded more nodes than A* (showing that it took UCS more computations to find an optimal path).
Rubric
| Item | Description | Points |
|---|---|---|
| A* | A* graph search correct and passes test cases | 35 |
| UCS | Uniform cost search correct and passes test cases | 10 |
| Tile heuristic | tile heuristic implemented correctly | 10 |
| Manhatten heuristic | The manhatten tile heuristic implemented correctly | 15 |
| Named tuples | Named tuples used on Frontier | 10 |
| Analysis plots | Plot of analysis on UCS, A* w/tile heuristic, and A* w/manhatten heuristic | 15 |
| Style | Good coding style | 5 |
Submitting
Submit your completed version of search.py, eightpuzzle.py
and a PDF containing your plots named searchPlots.pdf
through Gradescope.
You have an unlimited number of submissions. Note that the autograder is not verifying
your plots and namedtuple portions of the assignment (these will be manually evaluated).
3 - Local Search Lab

Introduction
In this lab, you will construct a hill climber that will solve the NQueens problem. This is a well known problem where n queens are placed on a Chessboard where no queen can “attack” another queen. Queens can move horizonally, vertically, and diagonally for any distance.
Files
-
SearchProblem.py a abstract class (well, as close as you can get in Python) that represents a search problem. Based on work from AIBerkley.
-
nqueen_hillclimber.py (UNFINISHED) Implements the NQueensProblem class, which includes code to compute the conflicts (heuristics function), successor functions, and goal state tests. It also includes some code to plot your results.
Instructions
Gradescope
Complete the local search lab in Gradescope first, which discusses the size of the state space for this problem.
Argument Passing
The code in nqueen_hillclimber.py contains the function parse_arguments.
This function utilizies python’s ArgumentParser object. It defines
a command line argument named nqueens that can passed in to specify
the dimension of the board.
python nqueen_hillclimber.py --nqueens 8
The parms object that is passed back will contain a variable for each parameter. You can access the argument in your code as parms.nqueens. There is also an argument called runs that controls the number of hill climbers that are executed.
Coding
Augment nqueen_hillclimber.py to utilize a steepest descent hill climber
as discussed in the reading assignment and in lecture. We refer to this as the descent version since the problem wants to drive the number of conflicts to zero.
NOTE: If the successor function returns many states with the same number
of conflicts, select randomly from the sublist of similar values.
Recall that you want to minimize the number of conflicts. When no state is better than the current state, you have reached an optimum value (and possibly a local optimum).
-
The starting state for this first test is with all the queens in the same column [0,0,0,0]. Does your program find a solution? Run your program 30 times and gather the number of attacking queens (the heuristic) when the optimum is reached and the number of moves/actions it took to find the optimum. What is this ratio of totalSuccess (when the number of conflicts equals zero) over the total number of attempts. Each run of your program should behave differently since you have a stochastic component of breaking ties when the heuristic function minimum has multiple values.
-
Change your program so that instead of starting at state [0,0,0,0], start at a random state. You can add a new function to the
NQueensProblemclass to support this.
Run your program 30 times and compute the same ratio as in the prior step. -
Determine the maximum value of n that your program can accept and complete within two minutes.
Python Tip
You can still use namedtuples here, and I would encourage that (although it is not requried here). If you want to unpack a function’s return value into a named tuple, you can use the _make function that is part of the namedtuple implementation.
State = namedtuple("State", "board hx")
current_state = State._make(qprob.getStartState())
Rubric
| Item | Description | Points |
|---|---|---|
| Gradescope Written Portion | Questions on NQueens state space | 3 |
| Code | Your code executes propertly when run and includes an example in the top of your program to show how to run it. | 6 |
| 3 Questions answered | Questions (ratios and max n) are clearly specified in a comment block at the top of your program | 3 |
Submitting
Submit your completed version of nqueen_hillclimber.py
through Gradescope to the Lab3 Coding problem.
Your answers to the 3 questions above should be embedded in
the top of your nqueen_hillclimber.py code as comments.
4 - Value Iteration Lab
Value Iteration Gridworld
Introduction
In this lab, you will construct the code to implement value iteration in order to compute the value of states in a MDP.
Files
-
valueIteration.zip
in a directory. In this lab, you will be changing the
valueIterationAgents.pyfile.
Coding
Construct code for a MDP that is computing using value iteration. You will need to code the following methods in valueIterationAgents.py:
runValueIteration. This method is invoked from the constructor.- computeQValueFromValues
- *computeActionsFromValues
Recall that the value iteration state update equation is: $$ V_{k+1} = \max_{a}\sum_{s’}T(s,a,s’)[R(s,a,s’) + \gamma V_{k}(s’)] $$
When implementing value iteration, you are only being asked to
run for the number of iterations requested on the command line (so, do not run until convergence).
The number of iterations to run value iteration is an argument (specified via the -i command option) and stored within self.iteration in the ValueIterationAgent class.
You should also look at the __init__ method, as it shows some VERY useful methods within
the self.mdp object that you will need. This is an offline planner.
Important:
- Use the “batch” version of value iteration where each vector $V_k$ is computed from a fixed vector $V(k-1)$ which is how this was described during lecture (not the “online” version we will discuss that is required for reinforcement learning). This means that when a state’s value is updated in iteration k based on the values of its successor states, the successor state values used in the value update computation should be those from iteration k − 1 (even if some of the successor states had already been updated in iteration k).
- A policy synthesized from values of depth $k$ (which reflect the next $k$ rewards) will actually reflect the next $k + 1$ rewards (i.e. you return $\pi(k+1)$. Similarly, the Q-values will also reflect one more reward than the values (i.e. you return $Q(k+1)$. You should return the synthesized policy $\pi(k+1)$.
- Hint: You may optionally use the
util.Counterclass inutil.py, which is a dictionary with a default value of zero. However, be careful with argMax: the actual argmax you want may be a key not in the counter! - Note: Make sure to handle the case when a state has no available actions in an MDP (think about what this means for future rewards).
- The docstring comments above the functions also mention this, but when no states are available do to a state being a terminal state, you can return that no actions are possible and the value is zero.
To test your implementation, run the autograder:
python gridworld.py -a value -i 100 -k 10
The following command loads your ValueIterationAgent, which will compute a policy and execute it 10 times. Press a key to cycle through values, Q-values, and the simulation. You should find that the value of the start state (V(start), which you can read off of the GUI) and the empirical resulting average reward (printed after the 10 rounds of execution finish) are quite close.
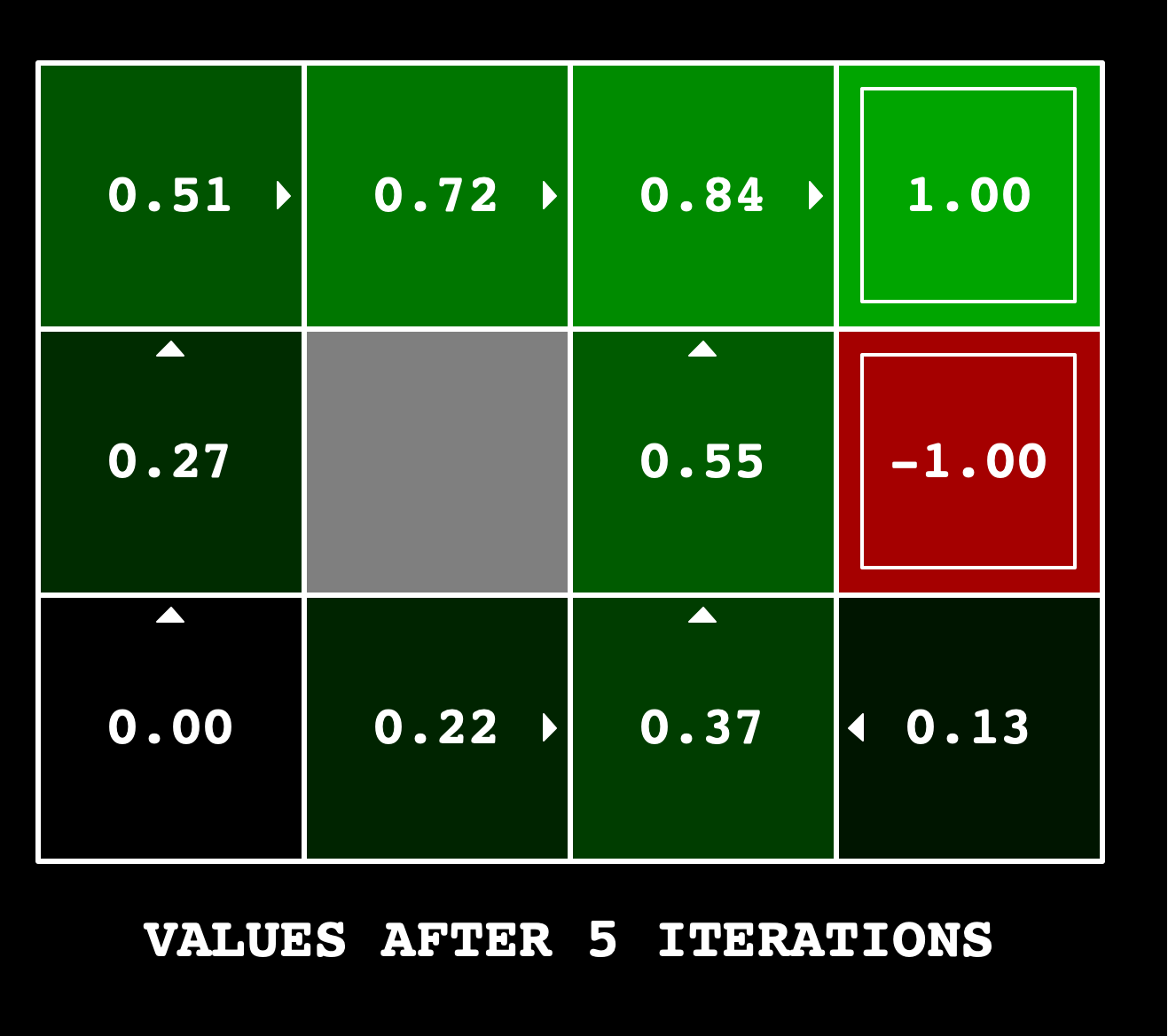
Running the following command should give the values that are shown at the top of this assignment.
python gridworld.py -a value -i 5
Grading:
| Project Part | Points |
|---|---|
| Autograder score | 23 |
| Code Review/Doc/Comments | 2 |
To run the autograder, you can use this command:
python autograder.py -q q1
Submitting
Submit your completed version of multiAgent.py
through Gradescope to the Value Iteration assignment.
However, you can test your code locally using the procedures listed above.