This is the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

Labs

1-Day In-Class Assignments

1 - Iterator Lab

Introduction

In this lab, you will review and create three iterators and submit the assignment through Gradescope.

Files

Download the following files:

Part 1 - Review an Iterator

Take a few minutes to read over the file BackScanner.java to make sure you understand how it works. You can test it using the provided driver (IteratorDriver.java)

Part 2 - Implement a Skip Iterator

Complete the SkipScanner.java file following the requirements put forth in the JavaDoc comments at the beginning of the file. You can test your iterator with the SkipScannerTest JUnit tests.

Part 3 - Implement a Skip Iterator with Generics

Make a copy of your working SkipScanner.java class to a new file named SkipScannerGeneric.java. Change the SkipScannerGeneric class so that instead of accepting an array of Strings it will accept an array containing any type of object.

Part 4 - Implement a NGram iterator

Complete the NGramScanner.java file following the requirements put forth in the JavaDoc comments at the beginning of the file. You can test your iterator with the NGramScannerTest JUnit tests.

Lab Submission

Submit the following files together in Gradescope:

  • SkipScanner.java
  • NGramScanner.java
  • SkipScannerGeneric.java

2 - Pair Generic Lab

Introduction

he goal of this lab is to explore key features of the Java collections framework. Collections are tailored to hold values of certain types through generic type parameters. Collection classes also provide iterators so that clients can loop through elements in a standard way.

Portions of this lab were developed by Dr. Michael Kirkpatrick with modifications by Dr. Chris Johnson.

Files

Download the following files:

Pair and PairTest

Your first task is to develop a generic `Pair`` class that represents a 2-tuple. A 2-tuple is a collection of two elements, a 3-tuple is a collection of three elements, and an n-tuple is a collection of n elements.

A Pair abstraction is useful when you need to store ordered pairs like Cartesian coordinates, names and quantities, latitudes and longitudes, keys and values, and so on. To make Pair versatile, you don’t want to overconstrain the types of the two components. You want the first component to be of any type, and you want the second component to be of any type. The two components may have the same or different types.

The downloaded Pair class is flexible: it can be used to store objects of any type. Unfortunately, it is both dangerous and inconvenient. It is dangerous because we may accidentally store an object of an unexpected type (as you saw above). It is inconvenient because we will usually need to cast objects retrieved from a Pair before they can be used.

We can address these issues by making our Pair class generic. Our improved class will accept two type parameters since we may want the type of the first element to be different from the type of the second. Complete the following steps. Follow these steps to build a generic Pair class and a set of unit tests:

  • Download files

  • Scan through Pair.java and PairTest.java. Run the unit tests and confirm that they pass—for the moment. You are about to change both files so that Pair uses generics instead of the meaningless Object class.

  • Change testPairCharacterInteger so the Pair is declared with type parameters Character and Integer. In other words, you don’t want this raw instance:

Pair pair = new Pair('B', 12);

You want this parameterized instance:

Pair<Character, Integer> pair = new Pair<>('B', 12);

  • The parameters are optional in the second <> because the compiler infers them from the variable declaration. The tests will no longer compile. That’s to be expected. A principle of test-driven development is that you write the test first, and the code to be tested second.

  • Edit Pair to use generics and pass the first test. Note that all occurrences of Object should be replaced with a generic parameter. The type Object should not appear anywhere in the finished class.

  • Eliminate the casts and value getters in the calls to assertEquals. Because of the generic parameter, the compiler knows the types and doesn’t need you to cast anything.

  • Implement testPairDoubleDouble and testPairStringInteger to perform appropriate tests for pairs of different component types. Make sure they pass. Note that assertEquals requires an extra tolerance parameter for doubles.

  • Modify the Pair class to use generics so that it passes these three tests. Note that all uses of Object should be replaced with a generic parameter. NOTE: The type of Object should NOT appear anywhere in the finished class.

  • Uncomment the remaining tests in PairTest and make sure they complete successfully.

Iterators

You have a versatile but typechecked Pair class. Now create another collection, an array of Pair. Follow the instructions inside the PairList.java file and complete the methods. The supporting files (PairListTest.java and PairListDriver.java) do not required any modification.

Why Not Generic Arrays

You cannot create an array of a generic type in Java. In the early days of the language, the Java designers decided that arrays could be subtypes of other array types, provided the elements followed a subtype relationship. Assigning an array of Integer`` to a reference of type Object[]``, for example, is perfectly legal:

Object[] somethings = new Integer[10];
somethings[0] = 17;

But assigning to a reference of type String[] is not because Integer is not a subtype of String:

tring[] strings = new Integer[10];  // fails to compile

Assigning the array to a supertype has a cost. The compiler can no longer detect that this code is dangerous because a String typechecks as an Object:

somethings[0] = "Hydrogen";

So, the Java designers decided to add checks at runtime. When an element is assigned, the Java virtual machine verifies that the new element is a subtype of the array’s element type. If not, it throws an ArrayStoreException. In this case, a String is not an Integer, and we see the exception. Now suppose you could make an array whose type depends on a generic parameter:

Object[] lists = new ArrayList<String>[10];  // only hypothetical

Because of the way Java implements generics, the generic parameter String is only known at compile time. It is effectively erased in the compiled bytecode (this is formally called type erasure). At runtime, then, the code behaves like this:

Object[] lists = new ArrayList[10];   // the generic is erased

The array’s element type is just plain ArrayList. Since the element type has been erased, assigning a different sort of ArrayList doesn’t generate an ArrayStoreException:

lists[0] = new ArrayList<Integer>();  // hypothetically legal

Being able to assign an ArrayList<Integer> to an array of ArrayList<String> would be bad news. Programmers wouldn’t be able to trust Java’s typechecking. So, the designers forbid you from creating an array of elements whose type depends on a generic. As a workaround, you may allocate a raw array but assign it to generic reference:

@SuppressWarnings("unchecked")
ArrayList<String>[] lists = new ArrayList[10];

The annotation is needed to disable the warning. Suppressing warnings is almost always a bad idea that you should avoid. Because the generics are present on lists, the compiler will catch any type mismatches at compile time.

Lets Use Generics

Take another look at the PairDriver.java file. Your IDE should now be showing multiple warnings indicating that you aren’t using the Pair class correctly: no type arguments are being provided.

Complete the following steps.

  1. Add type arguments so that the Pair instances all have String for the first object and Integer for the second.
  2. STOP and THINK After adding the generics, can you remove the explicit casting in largestStadium? Why or why not? If you can, then go ahead and do so.

Lab Submission

Submit the following files together in Gradescope:

  • Pair.java
  • PairTest.java
  • PairDriver.java
  • PairList.java

3 - Big-Oh Analysis Lab

Introduction

Practice the computation of \(\mathcal{O}\) from source code.

Problem 1

To determine the number of steps, count all assignments to sum.

public static int someFunc1(int[] numbers) {
    int sum = 0;

    for (int num : numbers) {
      sum += num;
      for (int i = 0; i < 20; i++) {
        sum += i;
      }
    }
    return sum;
  }

Answer these questions:

  1. Is there a different between worse-case and every-case?
  2. State the exact growth function
  3. proof its membership into its complexity class.

Problem 2

To determine the number of steps, count all assignments to sum.

public static int fun(int[] numbers) {
    int sum = 0;

    for (int i = 0; i < numbers.length; i++) {
      sum += numbers[i];
      for (int j = i; j < numbers.length; j++) {
        sum += numbers[i] * numbers[j];
      }
    }
    return sum;
  }

Answer these questions:

  1. Is there a different between worse-case and every-case?
  2. State the exact growth function
  3. proof its membership into its complexity class.

Problem 3

To determine the number of steps, count all assignments to s.

PROCEDURE DoStuff(numbers1, numbers2)
    s <- 0
    
    FOR x IN numbers1 DO
      FOR y IN numbers2 DO
         IF x < y DO
           RETURN 0
         ELSE
           s <- s + x
         ENDIF
       ENDFOR
    ENDFOR
    
    FOR x IN numbers2 DO
      s <- s + x
    ENDFOR
    
    RETURN s

Answer these questions:

  1. Is there a different between worse-case and every-case?
  2. How should the input size be represented?
  3. State the exact growth function
  4. proof its membership into its complexity class.

Problem 4

Consider the following code:

public static int fun3(ArrayList<Integer> nums1, ArrayList<Integer> nums2) {

    int overlap = 0;
    for (int num : nums1) {
      if (nums2.contains(num)) {
        overlap++;
      }
    }
    return overlap;
  }

Answer the following questions:

  1. State what is an appropriate basic operation that you will be using to count the number of steps.
  2. State the exact growth function
  3. proof its membership into its complexity class.

Problem 5

Use incrementing sum as the basic operation. For the sake of simplicity, you may assume that the length of numbers is a power of 2.

public static int fun4(int[] numbers) {
    int sum = 0;
    for (int i = numbers.length - 1; i >= 1; i /= 2) {
      for (int j = 0; j < numbers.length / 2; j++) {
        sum++;
      }
    }
    return sum;
  }

Answer the following questions:

  1. Is there a different between worse-case and every-case?
  2. State the exact growth function
  3. proof its membership into its complexity class.

Problem 6

public static int fun5(int[] numbers) {
    int sum = 0;
    for (int i = 0; i < numbers.length; i++) {
        flibbert(numbers); // We know that flibbert requires fewer than
                           // n^2 operations in the worst case. 
    }
    return sum;
  }

Answer the following questions:

  1. Is there a different between worse-case and every-case?
  2. State the exact growth function
  3. proof its membership into its complexity class.

Lab Submission

If you are in class, there is nothing to submit (its a participation grade). If you are not in class, you must submit a scanned sheet with the answers to the 6 questions by the due date.

4 - Dynamic Analysis Lab

Introduction

Practice run time analysis on the following code snippets.

Problem 1

To determine the number of steps, count all assignments to sum.

/*
 * What is the big-Theta running time of this method, assuming 
 * that list is
 * 
 * an ArrayList:
 * 
 * a LinkedList:
 * 
 */
public static int sumByIndex(List<Integer> list) {

    int sum = 0;
    for (int i = 0; i < list.size(); i++) {
        sum += list.get(i);
    }
    return sum;
}

Problem 2

To determine the number of steps, count all assignments to sum.

/*
 * What is the big-Theta running time of this method, assuming 
 * that list is:
 * 
 * an ArrayList:
 * 
 * a LinkedList:
 * 
 */
public static int sumWithIterator(List<Integer> list) {

    int sum = 0;
    for (int curValue : list) {
        sum += curValue;
    }
    return sum;
}

Problem 3

/*
 * What is the big-Theta running time of this method, 
 * assuming that toList is initially empty, and that both lists are 
 * of type:
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copy(List<Integer> fromList,
                        List<Integer> toList) {

    for (int item : fromList) {
        toList.add(item);
    }
}

Problem 4

Consider the following code:

/*
 * What is the big-Theta running time of this method, assuming
 * that toList is initially empty, and that both lists 
 * are of type:
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copyReverseA(List<Integer> fromList, 
                                List<Integer> toList) {

    for (int item : fromList) {
        toList.add(0, item);
    }
}

Problem 5

/*
 * What is the big-Theta running time of this method, assuming that
 * toList is initially empty, and that both lists are of type
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copyReverseB(List<Integer> fromList, 
                                List<Integer> toList) {
    int value;
    for (int i = fromList.size() - 1; i >= 0; i--) {
        value = fromList.get(i);
        toList.add(value);
    }
}

Problem 6

/*
 * What is worst-case the big-Theta running time of this method,
 * assuming that toList is initially empty, and that both lists
 * are of the indicated type. Describe the worst case.
 * 
 * 
 * ArrayList:
 * 
 * 
 * LinkedList:
 * 
 * 
 * What is average-case the big-Theta running time of this method, 
 * assuming that toList is initially empty, and that both lists 
 * are of the indicated type.
 * 
 * 
 * ArrayList:
 * 
 * 
 * LinkedList:
 * 
 * 
 */
public static void copyScramble(List<Integer> fromList, 
                                List<Integer> toList) {

    Random gen = new Random();
    int randomIndex;
    int value;
    for (int i = 0; i < fromList.size(); i++) {
        randomIndex = gen.nextInt(fromList.size());
        value = fromList.remove(randomIndex);
        toList.add(value);
    }
}

5 - Dynamic Arrays Lab

Introduction

Dynamic arrays allow for expansion when their capacity limit is reached. In this lab, you will modify the openDSA list to provides these capabilities.

Files

Download the following files:

Part 1 Dynamic Arrays (95%)

Dynamic arrays use the following algorithm to ensure sufficient capacity when new elements are added:

if the current array is full:

  • Allocate a new array that is twice as large as the current array.
  • Copy all entries from the current array to the new array.
  • Replace the current array with the newly allocated array.

Your goal for this lab is to update the OpenDSA AList class so that it performs these steps every time append or insert is called. Since the same steps are required for both methods, it would be appropriate to create a private helper method.

Part 2 Shrinking Arrays Too (5%)

The resizing operation above provides an efficient mechanism for ensuring that the AList always has adequate capacity. However without a corresponding mechanism for shrinking the array the AList might end up tying up a huge amount of unneeded memory. Imagine adding 1,000,000 items, then immediately removing them.

One solution for this problem is to monitor the percentage of the array that is currently being used, and to resize the array if the value falls below some threshold.

Modify the remove method so that it shrinks the array by a factor of 2 whenever the number of used entries falls below 25%.

BONUS QUESTION #1: Why 25% and not 50%?

BONUS QUESTION #2: The designers of the Java ArrayList class chose not to implement this shrinking operation. What do you think motivated their decision?

Lab Submission

Submit AList.java to Gradescope:

6 - Linked List Lab

Create a double linked list structure.

Files

Download the following files:

Part 1 - Review an Iterator

Complete the unfinished iterator methods in DoubleList.java so that they satisfy the requirements of the Iterator Interface.

Part 2: Additional List Methods

Implement the following methods:

  • add(int index, E item)
  • remove (int index)
  • reverse()

Lab Submission

Submit DoubleList.java to Gradescope:

7 - Queue Lab

Introduction

The goal in this lab is to create two implementations of a queue. Complete the unfinished methods in LinkedQueue.java and ArrayQueue.java .

Files

Download the following files:

Lab Submission

Submit LinkedQueue.java and ArrayQueue.java to Gradescope.

8 - Recursion Lab

Introduction

Your goal in this lab is to gain more experience solving computational programs with recursion. You will write recursive solutions for three programming challenges.

Part 1: Collatz

The Collatz Conjecture is the claim that any integer greater than 1 will be reduced to 1 if you apply the following transformation: halve the number if it’s even, or triple the number and add 1 if it’s odd. Keep repeating the transformation on the resulting number until you arrive at 1.

The conjecture has not been proven true or false. However, it is true for all the numbers that have been tested. If you start at 10, the transformations lead to this sequence: 10 5 16 8 4 2 1. The Collatz count for 10 is 6, since it takes 6 steps to arrive at 1. If you start at 11, the transformations lead to this sequence: 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1. The Collatz count is 14.

Write class Collatz with a static method collatzCount. It accepts an int parameter for the number to transform. It returns the number of transformations needed to reach 1. If the number is already 1, the number of transformations is 0.

Solve this with recursion, not iteration.

Part 2: Pascal

Pascal’s Triangle is a visualization of the coefficients of the expansion of \((x+y)^n\). When \(n\) is 0 is 1, the expansion is 1. When \(n\) is 1, the expansion is \(1x + 1y\) . When \(n\) is 2, the expansion is \(1x + + 2xy + 1y\) .

The coefficients for all values of in [0, 6] are laid out in the rows of this truncated version of Pascal’s Triangle:

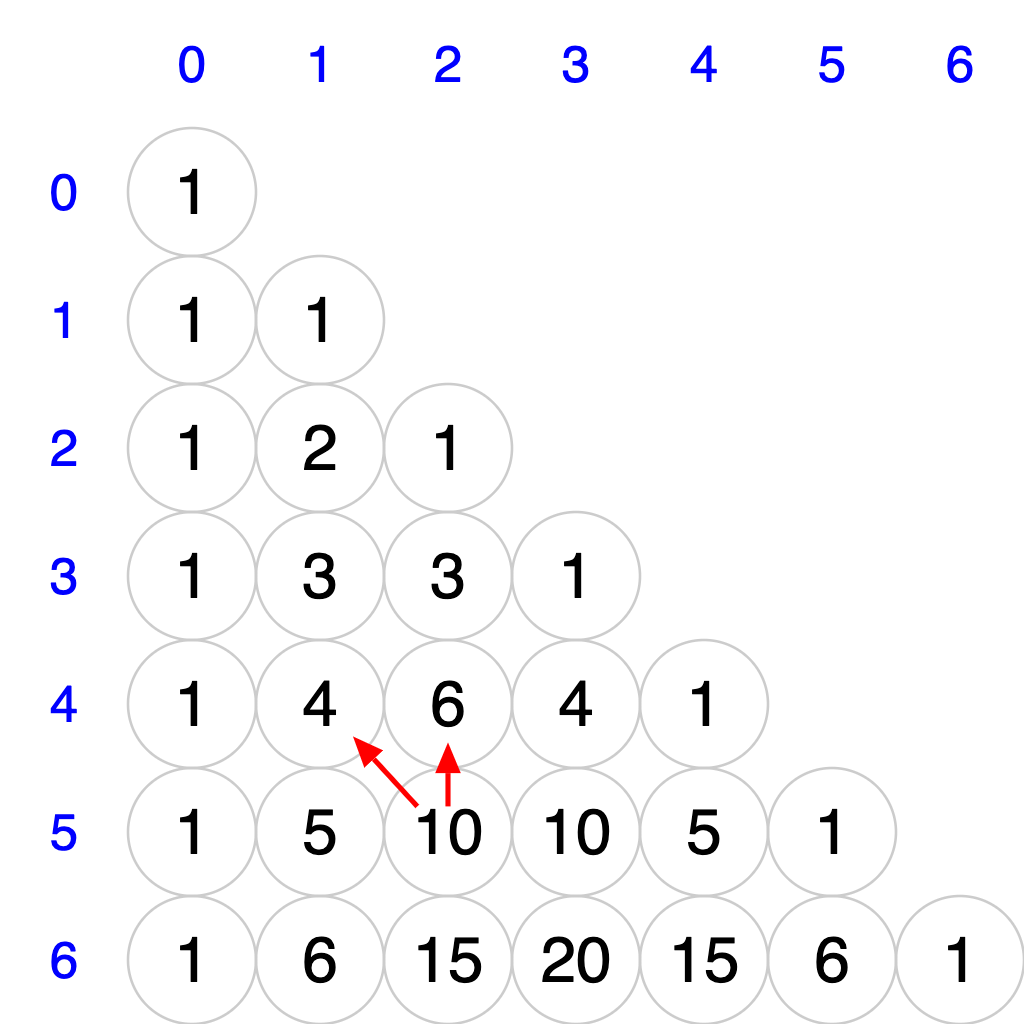
Create a class Pascal with a static recursive method pascal. It accepts a row and column of Pascal’s Triangle, both of type int, and it returns the coefficient at that row and column. The coefficient at a particular location is the sum of the coefficients to the north and northwest. Consider any value outside the triangle to be 0.

Solve this with recursion, not iteration.

Part 3: Box

Suppose you have a colored box that contains other colored boxes. These other boxes may in turn contain colored boxes. The twice-nested boxes may contain more boxes still. And so on. You are looking for a box of a particular color, so you go looking through this mess.

Write class Box with this public interface:

  • A constructor that accepts two parameters: a color name as a String and a List of its nested boxes.

  • search – The search method must accept a single String parameter representing the color of the box to search for. It must return null if the a box with that color could not be found, or a LinkedList containing the sequence of box colors from the outermost box to a box of the appropriate color.

Suppose you have this nesting structure:

  • red
    • yellow
      • pink
      • orange
      • blue
    • purple
      • mauve
      • cyan

If you call search on the red box to find orange, you’ll get back the list [red, yellow, orange].

Solve this with recursion and just a little bit of iteration to visit the nested boxes within a particular level.

This main method builds the above hierarchy of boxes and searches for orange:

public static void main(String[] args) {
  Box pink = new Box("pink", List.of());
  Box orange = new Box("orange", List.of());
  Box blue = new Box("blue", List.of());
  Box mauve = new Box("mauve", List.of());
  Box cyan = new Box("cyan", List.of());
  Box purple = new Box("purple", List.of(mauve, cyan));
  Box yellow = new Box("yellow", List.of(pink, orange, blue));
  Box red = new Box("red", List.of(yellow, purple));

  System.out.println(red.search("orange"));
}

Lab Submission

Your instructors are not providing the source code for JUnit tests in this lab. When your instructors provide tests, students often do not test code themselves and enter a frustrating game of trying to satisfy the grading machine. Please don’t do that. Test your code locally. Reason about its correctness. When you are reasonably confident in your solution, submit your code to Gradescope to run the autograder’s unit tests.

Submit Collatz.java, Pascal.java, and Box.java to Gradescope.

9 - Recurrence Lab

Introduction

Your goal in this lab is to gain more experience solving recurrences.

Exercise 1

Develop a recurrence and use the method of backward substitution to determine the number of multiplication operations that will be performed by the following method.

public static int fun(int n) {
        if (n == 0) {
            return 5;
        } else {
            int sum = 1;
            for (int i = 0; i < 4; i++) {
                sum *= 2;
            }
            return sum * fun(n - 1);
        }
    }
}

Exercise 2

Develop a recurrence and use the method of backward substitution to determine the number of array accesses performed by the following function.

FUNCTION fun4(numbers: array)
    RETURN fun4helper(numbers, numbers.length - 1)
    
FUNCTION fun4helper(numbers: array, index: integer)
    IF index = 0
        RETURN numbers[index]
        
    sum := 0
    
    FOR i =  0 to index
        sum := sum + numbers[index]
        
    RETURN sum + fun4helper(numbers, index - 1)

Exercise 3

Develop a recurrence and use the method of backward substitution to determine the number times the body of the inner loop is executed in the following method. (For the purpose of analysis, you may assume that the length of numbers is a power of 2)

public static int fun3(int[] numbers) {
    return fun3(numbers, numbers.length);
}

private static int fun3(int[] numbers, int index) {
    if (index <= 1) {
        return 3;
    }

    for (int i = 0; i < 4; i++) {
        fun3(numbers, index / 2);
    }

    int sum = 0;
    for (int i = 0; i < index; i++) {
        for (int j = 0; j < index; j++) {
            sum += numbers[i] + numbers[j]; //count this
        }
    }
    return sum;
}

Lab Submission

If you are in class today, there is nothing to submit. If you were absent, you must submit your work to Canvas by the due date.

10 - Expression Trees and Tree Traversals Lab

Any arithmetic expression can be represented as a tree structure where the internal nodes are operators and the leaf nodes are numbers.

Introduction

Any arithmetic expression can be represented as a tree structure where the internal nodes are operators and the leaf nodes are numbers. For example, the expression ((7.0 × 2.0 ) − (8.0 ÷ 2.0)) can be represented with the following tree:

In this lab you will complete the implementation of a binary tree that represents mathematical expressions in this way. This implementation will provide functionality for evaluating expressions and formatting them in prefix, postfix or infix notation.

Files

Before you start coding, carefully read each of the following files to make sure you understand their roles.

Object Oriented Traversals

Our textbook provides the following sample implementation of a pre-order traversal:

static <E> void preorder(BinNode<E> rt) {
  if (rt == null) return; // Empty subtree - do nothing
  visit(rt);              // Process root node
  preorder(rt.left());    // Process all nodes in left
  preorder(rt.right());   // Process all nodes in right
}

In this code, the traversal has been implemented as a static method in some separate class that is passed a reference to a root node. As an alternative, it is possible to implement a tree as a recursive data structure without a separate class to handle the traversals. In this approach the node is the tree, and all of the functionality is implemented through methods of the node class. Our ExpressionNode class will be organized in this way. Under this approach, a preorder traversal might look like the following:

private void preorder() {
  visit();                // Process root node
  if (!isLeaf()) {
    left().preorder();    // Process all nodes in left
    right().preorder();   // Process all nodes in right
  }
}

It may seem odd to see a recursive method with no (apparent) arguments. In this case the argument is implicit. Since the recursive calls are executed on different BinNode objects, it is the object this that changes from one call to the next.

Note that the method above will only work for full binary trees: it assumes that every node is either a leaf, or contains two valid children. Our expression trees will necessarily be full because every operation must have exactly two operands. The methods for our ExpressionNode classes will be even simpler than the traversal above. Since leaves are stored in a a different node type, there is no need for an explicit isLeaf check .

Lab Submission

Submit OperatorNode.java through Gradescope . You are not required to compete PrefixParser, but you should do so if you have time.

11 - Binary Search Tree Activity

Complete the following problems.

Problem 1

This is not a valid binary search tree. What is wrong with it?

     32
    /  \ 
   16  45
  /  \
 5   38

Problem 2

Use the Binary Search Tree insertion algorithm to insert the keys: 1, 2, 3, 4, 5, 6, 7 into an initially empty BST (in that order!).

Height

What is the height of the tree?

/*
 * What is the big-Theta running time of this method, assuming 
 * that list is
 * 
 * an ArrayList:
 * 
 * a LinkedList:
 * 
 */
public static int sumByIndex(List<Integer> list) {

    int sum = 0;
    for (int i = 0; i < list.size(); i++) {
        sum += list.get(i);
    }
    return sum;
}

Problem 2

To determine the number of steps, count all assignments to sum.

/*
 * What is the big-Theta running time of this method, assuming 
 * that list is:
 * 
 * an ArrayList:
 * 
 * a LinkedList:
 * 
 */
public static int sumWithIterator(List<Integer> list) {

    int sum = 0;
    for (int curValue : list) {
        sum += curValue;
    }
    return sum;
}

Problem 3

/*
 * What is the big-Theta running time of this method, 
 * assuming that toList is initially empty, and that both lists are 
 * of type:
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copy(List<Integer> fromList,
                        List<Integer> toList) {

    for (int item : fromList) {
        toList.add(item);
    }
}

Problem 4

Consider the following code:

/*
 * What is the big-Theta running time of this method, assuming
 * that toList is initially empty, and that both lists 
 * are of type:
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copyReverseA(List<Integer> fromList, 
                                List<Integer> toList) {

    for (int item : fromList) {
        toList.add(0, item);
    }
}

Problem 5

/*
 * What is the big-Theta running time of this method, assuming that
 * toList is initially empty, and that both lists are of type
 * 
 * ArrayList:
 * 
 * LinkedList:
 * 
 */
public static void copyReverseB(List<Integer> fromList, 
                                List<Integer> toList) {
    int value;
    for (int i = fromList.size() - 1; i >= 0; i--) {
        value = fromList.get(i);
        toList.add(value);
    }
}

Problem 6

/*
 * What is worst-case the big-Theta running time of this method,
 * assuming that toList is initially empty, and that both lists
 * are of the indicated type. Describe the worst case.
 * 
 * 
 * ArrayList:
 * 
 * 
 * LinkedList:
 * 
 * 
 * What is average-case the big-Theta running time of this method, 
 * assuming that toList is initially empty, and that both lists 
 * are of the indicated type.
 * 
 * 
 * ArrayList:
 * 
 * 
 * LinkedList:
 * 
 * 
 */
public static void copyScramble(List<Integer> fromList, 
                                List<Integer> toList) {

    Random gen = new Random();
    int randomIndex;
    int value;
    for (int i = 0; i < fromList.size(); i++) {
        randomIndex = gen.nextInt(fromList.size());
        value = fromList.remove(randomIndex);
        toList.add(value);
    }
}

12 - AVL Tree Lab

Introduction

Problem 1

Label the following BST with AVL balance factors. Is this a properly balanced AVL tree?

Problem 2

Show how the AVL tree below changes when the following operations are applied (in order).

  • insert(B)
  • insert(A)
  • insert(F)
  • insert(E)`

Start with this tree:

Problem 3

Imagine that 1,000,000 (\(\approx{2^{20}}\) ) keys are added to an initially empty AVL tree. Which of the following could be the height of the resulting tree? (Recall that, for any binary tree, \(h(n) \ge \lfloor log_2 n \rfloor \), and for an AVL tree: \(h(n) \lt 1.44 log_2 (n+2) - .328\) )

  • 10
  • 15
  • 20
  • 25
  • 50
  • 100
  • 1000
  • 1000000

Problem 4

Consider the following sorting algorithm:

TreeSort(array)
    -- Insert all items from the provided array into an initially 
       empty AVL tree.
    -- Perform an in-order traversal of the tree, copying all items
       back into the provided array.

  • What is the worst-case big-\(\Theta \) running time of this algorithm?

  • Is it in-place?

  • Is it stable?

Lab Submission

If you are in class, please submit a copy of your sheet to canvas (just take a picture). If you are not in class, you must submit a scanned sheet with the answers to the questions by the due date.

13 - BST Search Lab

Introduction

The goal in this lab is to utilize a binary search tree for performing different types of search operations.

Files

Download the following files:

Lab Submission

Submit BSTDictionary.java to Gradescope.

14 - 16 - Hash Table

Introduction

Files

Download the following files:

Instructions

Before diving in, scan through the code to see what state, methods, and helper classes are available. Then complete these tasks:

  • Implement the findKey helper method. Use open addressing with linear probing to resolve collisions. If the probe encounters a previously deleted item, continue on to the next bucket as described in the textbook. This helper method should be used by put, get, and remove.

  • Implement put. The findKey helper method can be used to determine if the key is already in the table. If so, the value should be replaced. If not, a new entry must be added to the table.

  • Implement get. If the key can’t be found, return null.

  • Implement remove. If the key can’t be found, return null. Don’t delete by nulling out the cell, as this action would break the probing sequence. Use the methods of Item instead.

  • Implement resize. Double the table size and migrate all the old, non-deleted items to the new table. You can’t just put the old items in the same cells, however, because an item’s position depends on the table size. Automatically resize the table if the load factor exceeds MAX_LOAD.

Lab Submission

Test each step as you complete it. Once you are confident your implementation is correct, submit HashTable.java through Gradescope.

15 - 17 - Graph Programming

Introduction

Files

Download the following files:

Instructions

Complete the unfinished methods in ArrayGraph.java and GraphAlgorithms.java. You can test your methods locally with the provided JUnit files.

Lab Submission

Test each step as you complete it. Once you are confident your implementation is correct, submit ArrayGraph.java and GraphAlgorithms.java through Gradescope.

16 - Application Lab

Introduction

The goal of this lab is to apply some of the techniques and structures we’ve studied this semester. You should read the problem descriptions, determine appropriate collection types, and implement efficient solutions. You should work in groups on this lab.

DO NOT RE-INVENT THE WHEEL! None of these problems require custom data structures; they can all be implemented efficiently using existing data structures from the Java Collections Framework. These include the following (among others):

Interface Hash Table Resizable Array Balanced Tree Linked List Hash Table + Linked List
Set HashSet TreeSet LinkedHashSet
List ArrayList LinkedList
Queue, Deque ArrayDeque LinkedList
Map HashMap TreeMap LinkedHashMap

Notably missing from the table is the PriorityQueue class.

Duplicate Tracker

Begin by downloading the following files:

Complete the methods of the DuplicateTracker class so that all operations are as efficient as possible. The purpose of this class is to process a sequence of user IDs such that duplicate IDs are identified and may be efficiently retrieved as a sorted List. You should assume that both the “add” and the “get” methods may be called arbitrarily many times and in any order: efficiency matters for both.

Here is a code snippet that illustrates the desired functionality:

    tracker.addID(5);
    tracker.addID(2);
    tracker.addID(1);
    tracker.addID(2);
    tracker.addID(5);
    tracker.addID(5);
    
    System.out.println(tracker.getDuplicates()); // Prints "[2, 5]"
    
    tracker.addID(1);
    
    System.out.println(tracker.getDuplicates()); // Prints "[1, 2, 5]"

You can test your implementation by executing the JUnit tests. These will run some tests for correctness as well as timing tests. Your goal is to pass all correctness tests with an overall execution time that is as small as possible.

Job Sequencer

Begin by downloading the following files:

Complete the methods of the JobSequencer class so that all operations are as efficient as possible. The purpose of this class is to process jobs of different types in the order that they are added to the system. Because there are a limited number of job handlers and they are specialized for a particular job type, you must make sure that the “nextJob” methods only return jobs of the requested type. You must also ensure that jobs of a particular type are processed in the order in which they arrived. You should assume that both the “addJob” and the “nextJob” methods may be called arbitrarily many times and in any order: efficiency matters for both.

Here is a code snippet that illustrates the desired functionality:

    JobSequencer sequencer = new JobSequencer();
    
    sequencer.addJob("A", 101);
    sequencer.addJob("B", 105);
    sequencer.addJob("A", 93);
    sequencer.addJob("B", 202);
    
    System.out.println(sequencer.nextJob("A")); // Prints "101"
    System.out.println(sequencer.nextJob("B")); // Prints "105"
    System.out.println(sequencer.nextJob("B")); // Prints "202"
    System.out.println(sequencer.nextJob("A")); // Prints "93"

Triage

Begin by downloading the following files:

Complete the methods in TriageTracker so that all operations are as efficient as possible. The purpose of this class is to prioritize patients as they seek health care. Each patient is entered into the system along with an integer priority value that quantifies the urgency of their medical condition. The nextPatient method should always remove and return the patient with the highest priority. In event of tied priorities, patients should be processed in the order they were added. The removePatient method makes it possible to remove a patient from the collection even if he or she has not been served.

    TriageTracker triage = new TriageTracker();
    
    triage.addPatient("01-A", 10); // Patient "01-A" has priority 10.
    triage.addPatient("02-A", 10);
    triage.addPatient("03-A", 1);
    triage.addPatient("04-A", 1);
    triage.addPatient("05-A", 10);
    triage.addPatient("06-A", 5000);
    
    triage.removePatient("02-A"); // Patient "02-A" got tired of waiting.
    
    System.out.println(triage.nextPatient()); // "06-A" (Highest priority)
    System.out.println(triage.nextPatient()); // "01-A" (First 10 priority)
    System.out.println(triage.nextPatient()); // "05-A" ("02-A" was removed!)
    System.out.println(triage.nextPatient()); // "03-A"
    System.out.println(triage.nextPatient()); // "04-A"

Neighbors

Complete the methods in NeighborCounter so that all operations are as efficient as possible. The purpose of this class is to maintain a collection of two-dimensional points and to determine how many points are within a particular distance from a query point. Duplicate points at the same location are not permitted.

    NeighborCounter nc = new NeighborCounter();
    
    // Add four points arranged in a square pattern:
    nc.addPoint(0.0, 0.0);
    nc.addPoint(0.0, 1.0);
    nc.addPoint(1.0, 0.0);
    nc.addPoint(1.0, 1.0);

    // All four points are within 1.0 of (.5, .5)...
    System.out.println(nc.numNeighbors(.5, .5, 1.0));  // Prints 4

    // No points are within .1 of (.5, .5)...
    System.out.println(nc.numNeighbors(.5, .5, 0.1));  // Prints 0

    // Only one point, (0, 0), is within .5 of (.1, .1)...
    System.out.println(nc.numNeighbors(.1, .1, .5));   // Prints 1

Lab Submission

Submit BSTDictionary.java to Gradescope.