PA - Expressions
Introduction
In this PA, you will apply your newly-minted Haskell expertise to the task of analyzing recursive data structures. Startup files are provided in a zip file below:
You may ignore Lexer.hs and Parser.hs. They were
auto-generated from grammar specification files using utilities called Alex and Happy, and they provide the backend
code for parsing simple mathematical expressions. Here is a context-free grammar
describing the langauge that this parser can recognize:
E -> <int>
| E + E
| E - E
| E * E
You may also ignore the definition of Token in
Defs.hs, although you will need to use the definition of the
Expr data type:
data Expr
= EInt Int
| EAdd Expr Expr
| ESub Expr Expr
| EMul Expr Expr
deriving (Show,Eq)
This data type represents nodes in the expression parse tree. For instance,
the expression "(2+3)*4" will be parsed into the following tree:
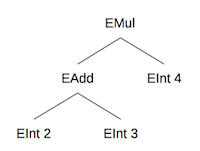
EInt, EAdd, ESub, and EMul are all data value
constructors, used to build or pattern match against an expression
tree. EInt represents an integer terminal node, while the other
three represent non-terminal arithmetic operation nodes. The last line of the
Expr definition specifies that we wish to be able to convert the
expressions to strings and compare them using Haskell built-in recursive
definitions.
Using these value constructors, we could represent the parse tree shown above with the following Haskell expression:
EMul (EAdd (EInt 2) (EInt 3)) (EInt 4)
You should convince yourself that this code represents a valid encoding of
the expression tree above. You may test this by loading Main.hs
into ghci and running the parse function, giving it
any string as an input. If it is a valid expression according to the grammar
specified above, the parse function will convert it into the
corresponding Haskell representation using the Expr data type and
its value constructors.
Your task in this PA will be to write various functions to analyze expression trees. You will do this by writing functions that recurse over an expression tree based on data patterns.
You can see an example of a pattern-based function in
formatExpr in Defs.hs. This function takes a tree and
matches it against one of the four different patterns possible using the value
constructors, returning a different form of string for each different pattern.
Most of the functions you write for this PA will have this general form. The function's input will be an expression tree, and you will specify the output of the function for each pattern that the input could be matched against. You will likely want to make recursive calls in the non-terminal cases.
If you look towards the bottom of Main.hs, you will see a bunch
of test functions. You should not change these functions in any way. If you load
this file into ghci as-is and run the main function, you will see that all the
tests fail. As you write your code, you can keep running main for an indication
of whether your code works. The column of numbers indicates how many tests you
are currently failing, and the sequences of "." and "X" indicate which tests are
passing and failing, respectively.
Functions
The functions you need to write are stubbed out in Main.hs.
Below are descriptions of them. You can also look at the test cases to see what
they are supposed to do. You should think about what the definition of each
function means for each Expr pattern.
-
eval :: Expr -> Int
Calculates the result of evaluating the mathematical expression. All operations should be done using integer arithmetic. -
countOps :: Expr -> Int
Counts the total number of arithmetic operations in an expression. All three operations (addition, subtraction, and multiplication) count for this process. -
height :: Expr -> Int
Calculates the height of the expression tree, where the height of a single-node tree is defined as being 1. -
postfix :: Expr -> String
Returns a flattened postfix string representation. For example,"(2+3)*4"in postfix notation would be"2 3 + 4 *". You should use(show i)"to convert integers to strings. -
uniqInts :: Expr -> [Int]
Extract a sorted list of all unique integers in an expression. Each integer should appear in the resulting list only once.
For the last function (uniqInts), you may find it helpful to
write two helper functions:
-
uniq :: Eq t => [t] -> [t]
Returns a copy of the given list with duplicates removed. -
sort :: Ord t => [t] -> [t]
Returns a sorted copy of the given list.
These helper methods (uniq and sort) are optional
and I will not be testing for them.
Deliverable Requirements
Submit ONLY your modified Main.hs file on
Canvas by 11:59 pm on Friday, March 6, 2015. Please fill in your name at the top
of the file. Do not modify the testing code or the main method.