kD-Tree PA
NOTE: Part of the objective for this project is to mimic what it's like to work on a software solution at a company. Typically, you will not be handed pseudo-code for every operation and subroutine you are supposed to program, but will instead be given a specification for a program--what inputs it should take and what outputs it should produce. You will then have to go figure out how to make it work.
For this project write-up, we are doing a bit of a hybrid approach. We are giving you some information on the kD-tree data structure (which you will be coding), but not everything you will need to know to code it. You are responsible for finding good additional information as needed in order to complete the project. Piazza discussions are especially encouraged.
For this reason, it is also important to read the entire project description and the provided code before you start working. Do not write a single line of code until you are sure you understand what is expected of you and how it fits into the framework of the code we've already given you. There is a lot to read, so make sure you start early!
Learning Objectives:
- Gain an appreciation for the power of binary trees and the types of operations a binary tree can support.
- Know how to code a particular type of binary tree called a kD-tree.
- Gain experience developing code from a less formal explanation of a data structure and its operations than full-fledged pseudo-code.
Getting Started
First download and decompress one of the starter files:
This PA has two major parts, and so these archives contain a large number of files. You will need to create Makefiles for both parts. Here is an overview of all the files:
The bst/ folder
This folder contains the bst.h/c files and the files needed for the bst/main tester program.
bst.h/c: The binary search tree files.drawtree.h/c: Tree drawing functions (uses turtle graphics).dynarray.h/c: Dynamic array (used for getting output from the range search function).main.c: The main test program.turtle.h/c: The turtle graphics library.
The kdtree/ folder
dynarray.h/c: Dynamic array (used for getting output from the range search functions).helpers.h/c: Contains a few helper structures and functions including thepoint_tandbbox_ttypes and functions for computing the distances between points.kdtree.h/c: The kD-tree implementation.main.c: The main tester program that generates a "screenshot" of the game.turtle.h/c: The turtle graphics library.
COMING SOON: The rangefighter/ folder
We will release this to you in the week after Thanksgiving. It contains the actual game code for rangefighter, which uses your kD-tree implementation as its main data structure.
Part 1: Range Finding in Binary Search Trees
You have seen in class how binary search trees (BSTs) are useful for supporting a find(x) operation that determines whether a value x is stored in the tree. Consider the following tree:
8
/ \
4 12
/ \ / \
2 6 10 14Let's recall what happens when we execute the command find(6). First find(x) looks at the root node to check if the value at the root node is equal to what we are looking for. It is not (6 != 8). Thus we need to recurse on one or the other of the subtrees. Because we have a BST, since 6 < 8, if 6 is to be found in the tree, it will have to be in the left subtree of 8. We thus search recursively on the left-subtree of 8 for 6.
Now let's generalize this idea a little. Instead of finding a specific value x, what if we wanted to find any value in a given range? For instance, what if we wanted to retrieve all values stored in the tree between 3 and 11? How would we implement this operation?
This operation is called range searching. We do not want to determine whether a particular value exists or not--as in the case of find(x)--but instead we want to find all values in the tree within the given range [3, 11].
To support this operation, we perform a recursive procedure that is very similar to the find(x) operation. Again, we start at the root node 8 and ask the question, "is 8 in our range [3, 11]?" The answer is, of course, yes, so we output 8. We then need to determine whether to continue searching recursively in the left subtree, the right-subtree, or both.
This is the main difference between the find operation and the range_search operation: in the find operation, there is always only one subtree we need to search in: either the left tree or the right. Now, however, there are three possible cases: 1) the range we are searching for can only possibly contain points from the left subtree, 2) it can only possibly contain points in the right subtree, or 3) it may possibly contain points from both. The third case arises precisely when the value of the current node is contained within the range. So in our case, because 8 itself falls inside the range [3, 11], both the left and the right subtrees may contain points that fall within the range. This means that we need to continue the search recursively in both subtrees.
So what does that look like? Well, let's first recurse on the left subtree. Since 4 is in [3, 11] we output the 4 and again we have to recurse on both the subtrees of 4. We first recurse on its left, 2, which is not in the range, so we do not output it. Since 2 has no children execution returns to 4 and we recurse down the right subtree. Here, 6 is in the range [3, 11], so we output 6. (If you are following along at home, we have now produced 8, 4, and 6 as output.) We have now finished with all branches of 4 and execution returns back to the recursive call at 8.
We now continue searching on the right child, 12. In this case 12 is not in the range [3, 11]. In fact, all possible values in the range [3, 11] are less than 12. This means that only the left-subtree of 12 can possibly contain any values that fall within [3, 11]. So instead of recursing on both the left and right subtrees, this time we will only continue our search in the left subtree of 12. When we recurse there, we find that 10 is in our range, and so we output it. We have now exhausted all subtrees we needed to search and the process terminates, having outputted 8, 4, 6, and 10, which are exactly those nodes of the tree with values in the range [3, 11].
Note that these values were not retrieved in order; however, we could easily modify this process to retrieve the values in order by changing the range_search function to use an inorder traversal instead of a preorder traversal.
Building a BST
Recall from class that the efficiency of operations on trees is often bound up with the height of the tree, and that is certainly the case here. In fact, the running time of the range search operation can be shown to be O(log n + k) on a BST with n nodes, where k denotes the number of elements in the tree that falls within the range. This is a little different than running times you have seen before, because the running time O(log n + k) is related to both the input size n and the output size k. This is called an output-sensitive run time.
To make sure that we get the log n term in the running time, our tree needs to be balanced. Suppose we have an array items of n integers we want to put in a BST. How can we build such a balanced tree? Here's a recursive idea. First select the median of the input array and make this the root node. Then build the left subtree from all the items in the array that are less than the median, and build the right subtree from all the items in the array that are greater than the median. We can do this reasonably efficiently by presorting the array. The steps look like this:
- Presort the
itemsarray to obtainsorted-items. - Select the median (
sorted-items[n/2]) and make it the value of the root node. - Recursively create the left subtree from
sorted-items[0:n/2-1]. - Recursively create the right subtree from
sorted-items[n/2+1:n].
Task 1: Implement a Range Search BST
Your first task is to implement a binary search tree (BST) structure equipped with the following operations found in the bst.c file in the bst/ folder in the starter code:
void bst_build(bst_t *tree, int array[], size_t length);The input parameters consist of an empty binary search tree and an unsorted integer array. This function should create nodes in
treein order to build a balanced binary search tree containing the elements fromarray.IMPORTANT: This function should run in O(n log n) time.
HINT: You will need a sort operation. You may use one of your sorting routines from PA4 or the built-in qsort method.
bool bst_find(bst_t *tree, int x);Returns true if the value
xis contained in the tree, false otherwise.IMPORTANT: This function should run in O(log n) time.
void bst_range_search(bst_t *tree, int range_min, int range_max, dynarray_t *output_array);This function takes as input a binary search tree, a range [range_min, range_max], and a dynamic array
output_array. It should perform the range search described above and add all items intreethat fall within the range to theoutput_array.IMPORTANT: This function should run in O(log n + k) time, where k is the number of points returned.
And of course, the usual memory management functions:
void bst_init(bst_t *tree);Initializes an empty binary search tree. (We have provided this for you.)
void bst_free(bst_t *tree);Frees any memory (i.e. the nodes) for this binary search tree.
NOTE: You will need a Makefile for the bst directory that builds the main program from the files found in the bst/ folder.
The ./main test program we have included should output the following to the console when run:
find(4)--should be true: true
find(10)--should be false: false
Items in [4, 12]: 7 9 12 4 5Furthermore, it should produce a turtle graphics image named output.bmp that looks like this:
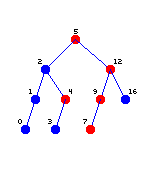
Output of bst main
Part 2: kD-Trees
A BST equipped with a range search operation as above is useful for many different applications. For instance, if we had a list of employees and wanted to answer queries like, "how many employees do we have between the ages of 20 and 25?" a BST would be a perfect data structure for supporting this type of query. However, what if we wanted instead to find all employees between the ages of 20 and 25 who make between 30 and 50 thousand dollars a year? A BST is not equipped to deal with this operation, because a BST only stores 1-dimensional data. Our query, however, is 2-dimensional, we want to query both an age range and a salary range. In order to handle such queries we need to generalize the binary search tree to higher dimensional data. We call this the kD-tree (where k is the dimension of the data).
For this PA you will not implement a full-blown kD-tree, but instead will implement a 2D-tree for handling 2-dimensional data.
Now our data, instead of being a list of numbers, like 8, 4, 12, 2, 6, 10, 14, is a list of 2D points. In the age/salary example, we could have the x-coordinates represent age and the y-coordinates represent salaries. So we might have, (23, 25000), (20, 55000), (50, 55000), (27, 95000), (24, 32000), (40, 28000), (35, 50000) as a list of employee age-salary "points". How can we store this using a tree? We could simply choose one of the dimensions, say the x dimension and simply build a normal BST on this dimension. Something like:
(27, 95000)
/ \
(23, 25000) (40, 28000)
/ \ / \
(20, 55000) (24, 32000) (35, 50000) (50, 55000)The problem with this approach is that we can still only support range search queries on the x-dimension.
Recall that we build a BST by recursively selecting the median, and then recursively building the left-subtree from all points less than the median, and the right-subtree from all points greater than the median. The key idea behind a kD-tree is to alternate which dimension we choose the median from each time we recurse.
In other words, if we are building a kD-tree age-salary points above, at the top level we would use the median of the age, we would then recurse and for the next level use the median of the salaries. At the following level we would again use the median of the age, and so on. The resulting tree looks like this:
(27, 95000) <-- median by age
/ \
(24, 32000) (35, 50000) <-- medians by salary
/ \ / \
(23, 25000) (20, 55000) (40, 28000) (50, 55000)For higher dimensional data, you continue with the same idea, every time you recurse in your build tree, just cycle through the available dimensions.
Range searching a kD-tree
Now that we have seen how to generalize a BST to 2-dimensional data, let's discuss the actual range searching. In 1 dimensional data, a range is just a range between two numbers, as we have seen. Something like [3, 11] which is all (1D) points lying between 3 and 11. There is no one right way to generalize this idea to 2-dimensional data. In fact, here are two possibilities that are equally natural:
- Box ranges: all points (x, y) such that x is in the range [xmin, xmax] and y is in the range [ymin, ymax]. This is called a box range, because the set of points fall within the box with corners (xmin, ymin), (xmin, ymax), (xmax, ymax), (xmax, ymin). See the image below.
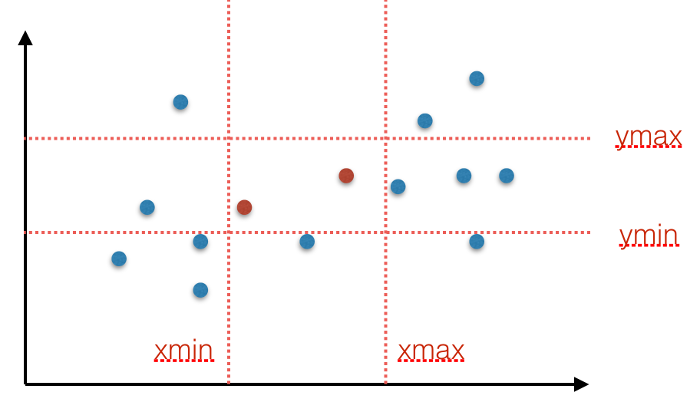
Box Range
- Circular ranges: all points (x, y) that fall within a circle centered at some point (cx, cy) with some radius r. See below.
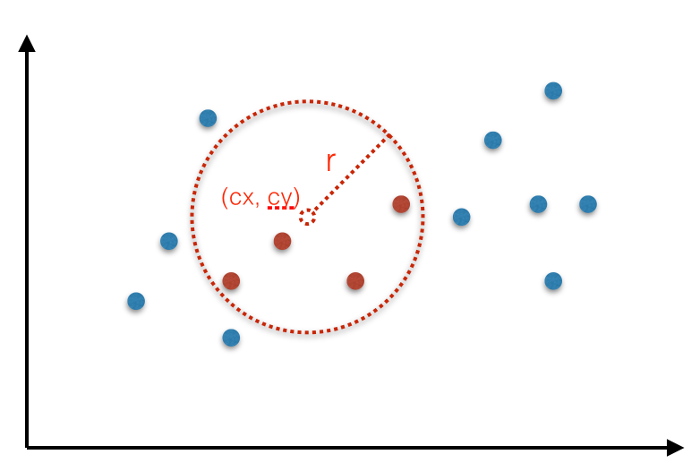
Circular range
Motivation: Range Fighter
Your second task is to implement a kD-tree for 2-dimensional points. To make things a little more interesting, you are going to be implementing this kD-tree to support a computer game based on the old Atari Asteroids game. The game is called "range fighter".
The player pilots a space ship through a debris field using the keys W, A, and D to move the ship forwards, left and right, respectively. The ship is equipped with two weapons. The first is a box range weapon that is activated by holding the space bar down. When the player hits the space bar, the box range weapon activates and a box is drawn from the initial position of the player when the space bar was pressed to the position of the player when the space bar was released. All of the debris within the box is destroyed when the space bar is released. The second weapon is a panic weapon that takes a long time to recharge but immediately destroys all debris within a certain distance of the player. It is activated by hitting the 'e' key.
Here is a screenshot of the game:
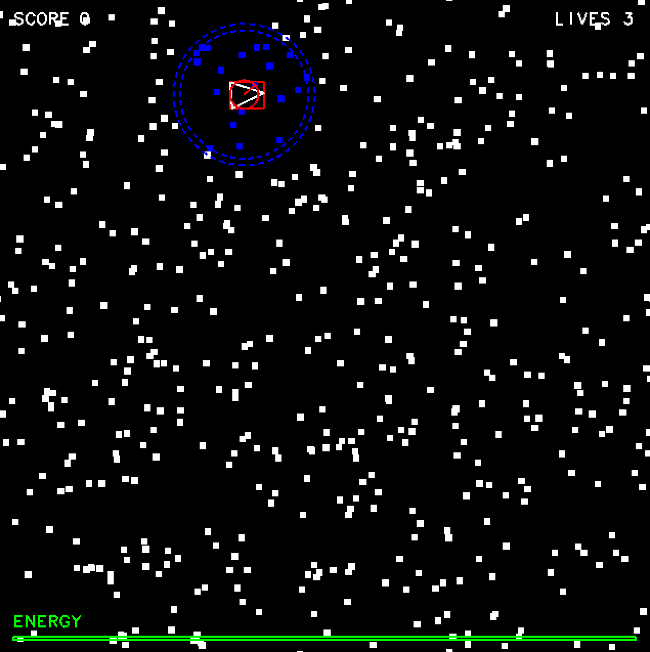
Game Screenshot
Your assignment is to implement a kD-tree for storing the debris field that supports both circular and box range searching operations. Rather than have you get started on a full-blown game (which might make debugging difficult!) we have provided a main program that uses turtle graphics to draw an image that looks like a screenshot from the game. You should first get your kd-tree working with this program, since it will be easier to debug. Once your kD-tree is working, you will be able to copy and paste your kdtree.c file into the game program code folder which we will give you the week after Thanksgiving.
Task 2: kD-Tree Implementation
All of the functions you need to implement are declared in the kdtree.h file and should be defined in kdtree.c. You may write helper functions in kdtree.c and declare them at the top of the file (but NOT in kdtree.h or your code won't compile when you submit it). For this assignment we have provided working iterator code, but you will not need to use iterators for any of this assignment. The iterators are there so that the main game application can use them. You need to implement the remaining functions in the kdtree library:
void kdtree_init(kdtree_t *tree)Initializes an empty kD-tree. (We have provided this for you.)
void kdtree_free(kdtree_t *tree)Frees a kD-tree.
void kdtree_build(kdtree_t *tree debris_t array[], size_t length)Builds a kD-tree with the
debris_tobjects inarray. This is essentially the same as thebst_buildoperation for BSTs except that it needs to alternate between using the x-coordinates adn the y-coordinates at each level of the tree for finding the median.IMPORTANT: This function should run in O(n log n) time.
HINT: You will need a sort operation. You may use one of your sorting routines from PA4 or the built-in qsort method.
void kdtree_box_range_search(kdtree_t *tree, bbox_t range, dynarray_t *debris_in_range)Adds all active debris that fall within the range to the dynamic array
debris_in_range.IMPORTANT: This function should run in O(log n + k) time, where k is the number of points returned.
HINT: How can you tell, at a given node, whether to recurse on the left or right subtree? Remember that at a given node we either split by x-coordinate, or we split by y-coordinate. Suppose the node represents an x-coordinate split. Then you are essentially doing the same check as in a 1D tree, where the range you are searching on is
[range.minx, range.maxx]. If the node represents a y-coordinate split, then you are checking they-coordinatesagainst the range[range.miny, range.maxy].HINT: In your recursive helper function you will probably need to track a depth in order to tell if you're looking at x- or y-coordinates.
void kdtree_circ_range_search(kdtree_t *tree, point_t p, float radius, dynarray_t *debris_in_range);Adds all active debris that fall within a distance of
radiusfrom the pointpto the dynamic arraydebris_in_range.IMPORTANT: This function should run in O(log n + k) time, where k is the number of points returned.
HINT: How can you tell, at a given node, whether to recurse on the left or right subtree? Remember that at a given node we either split by x-coordinate, or we split by y-coordinate. In the first case, we should first check whether the center of the circle lies to the left or the right of the x-coordinate of node's data. If it is to the left, then we definitely have to search the left subtree. If it is to the right, then we definitely have to search the right subtree. The question then is when do we have to search the other subtree as well. We must do this only if the absolute value of the difference in the x-coordinates of point
pandnode->debris.posis less than theradius, because otherwise, the circle centered atpwith radiusradiusis completely contained on one side of the split. (If this node represents a y-coordinate split, then this the discussion above is the same except for using y-coordinates instead of x-coordinates.)HINT: In your recursive helper function, you will probably need to track a depth in order to tell if you're looking at x- or y-coordinates.
Each piece of debris is represented by a debris_t object, which is defined in helpers.h in the kdtree/ folder. A debris_t object stores a 2D point named .pos for its coordinates and also stores a boolean value .active for whether the debris is active in the debris field or has been destroyed. Your kD-tree will store debris_t objects.
The helpers.h file also contains a few helpful types, such as bbox_t, which is used to define an axis-aligned bounding box for all points with x-coordinate between .minx and maxx and all points with y-coordinate between .miny and .maxy. It also defines point_t, which is used to specify a single 2D point.
Suggested Progression
First create a Makefile in kdtree/, get the code compiling, and run ./main. You should get the following output rangefighter.bmp:
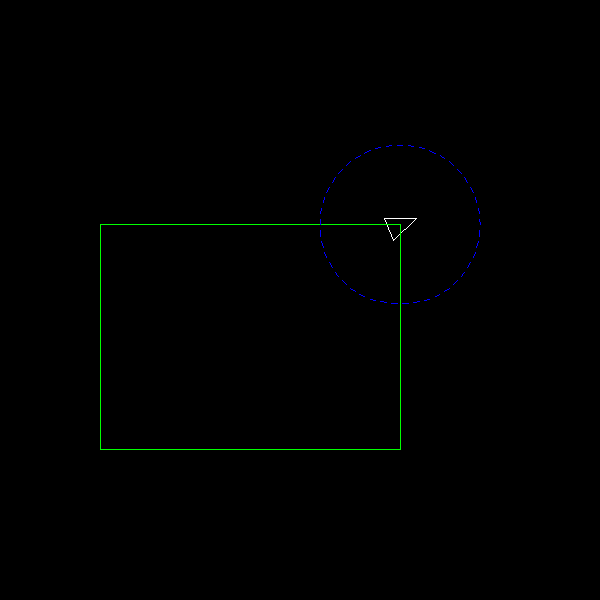
Initial Output
Next, implement the memory management and build-tree functions. Once these are working your output rangefighter.bmp should look like:
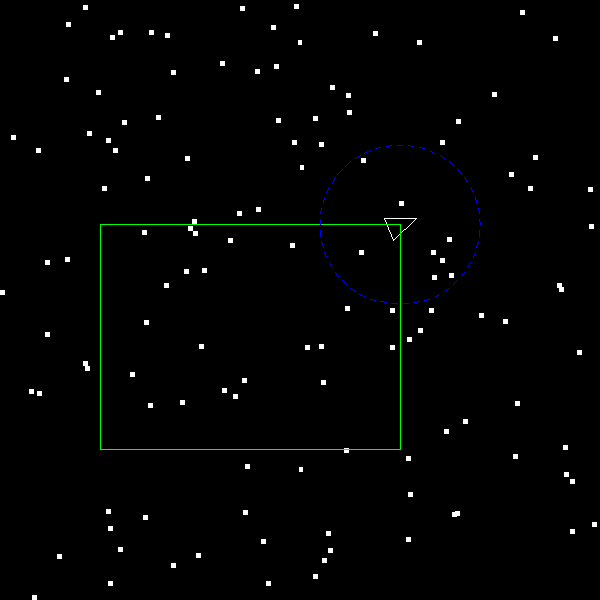
Tree is built!
Next, implement the box range searching. Once this is working you should see this:
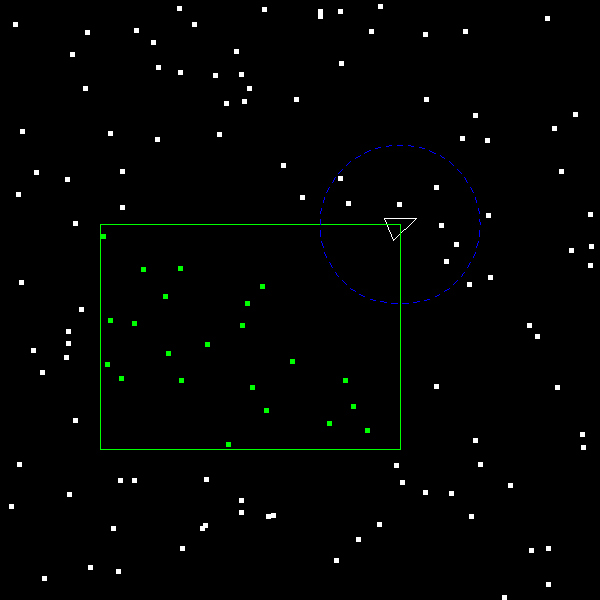
Box search is built!
Notice how all the debris within the green box is now highlighted green. The pieces of debris are randomly-generated, so the field will look slightly different every time you run the program, but all debris inside the box should be green regardless of their exact location.
Finally, get the circular range search working and the debris within the blue circle should appear blue:
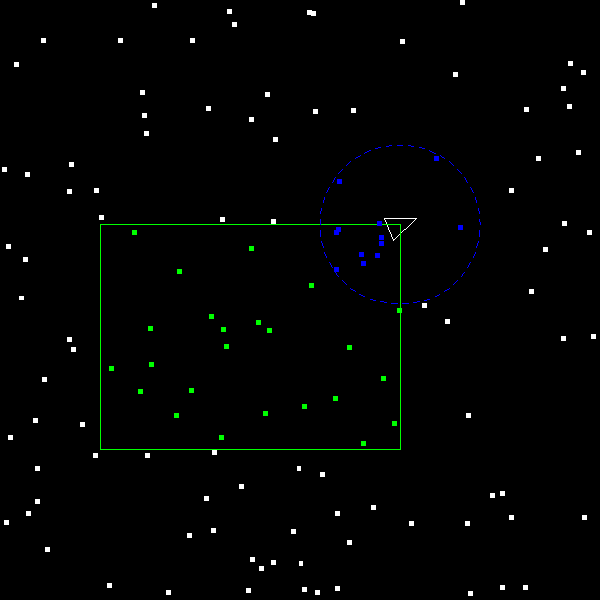
Everything is working, yay!
If you are having trouble debugging your code, you may wish to enable the call to draw_kdtree in main. This should give you a graphical representation of your kD-tree:
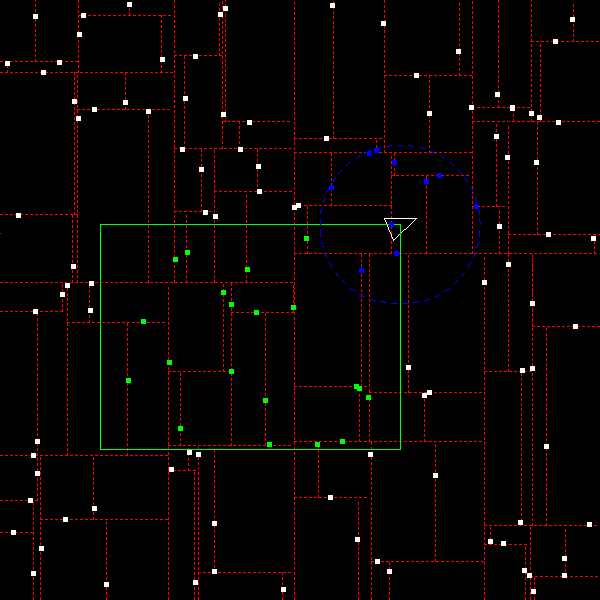
kD-trees are cool!
HINT: For debugging purposes, it can also be useful to temporarily lower the number of pieces of debris. You can do this by modifying debris_count in the create_random_debris_tree function. Here is what it looks like with only 16 pieces of debris:
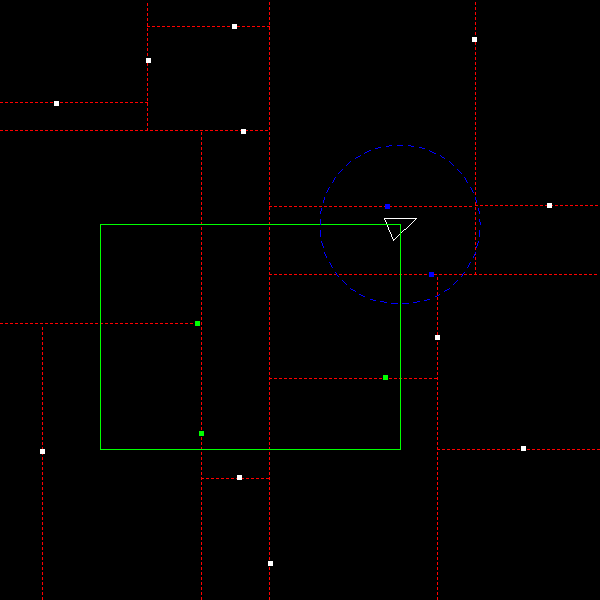
Fewer pieces of debris
Final Submission
DUE DATE: Friday, December 11, 2015 at 23:59 EST (11:59pm)
Submit ONLY your completed bst.c and kdtree.c files on Canvas using the appropriate assignment submission. Make sure the files contain a comment field at the top with your name and a statement of compliance with the JMU honor code.
IMPORTANT: There should be NO memory leaks in any of the code you submit for this assignment (both parts). You should test this using valgrind on both main programs.
Please check your code carefully and make sure that it complies with the project specification. In addition, make sure that your code adheres to general good coding style guidelines. Fix any spelling mistakes, incorrect code formatting, and inconsistent whitespace before submitting. Make sure you include any appropriate documentation.