CS240 - PA4

PA4: Sorting Improvements

Introduction

Quick sort is the fastest known comparison-based sorting algorithm when applied to large, unordered, sequences. It also has the advantage of being an in-place (or nearly in-place) sort. Unfortunately, quick sort has some serious failings: it's worst-case performance is O(n²), and it is not stable. Merge sort shares neither of these disadvantages: it is stable and it requires O(n log n) steps in the worst case. Unfortunately, merge sort requires O(n) additional space and it runs more slowly than quick sort on most inputs.

What we really want is a sorting algorithm that is as fast as quick sort, stable, in-place, with O(n log n) worst-case performance. Sadly, no such algorithm has yet been discovered. In practice, most code libraries follow one of two paths: either they provide a modified version of quick sort that is able to avoid worst-case behavior on typical inputs, or they provide a modified version of merge sort that is able to close some of the performance gap through careful optimizations.

The second approach has recently become popular. Both Python (starting in version 2.3) and Java (starting in version 7) use Timsort as their default sorting algorithm. Timsort is a modified version of merge sort that includes several enhancements: it uses a more space-efficient merge operation, it takes advantage of partially sorted arrays by finding and merging exiting sorted regions, and it uses a non-recursive binary insertion sort to handle short unsorted regions.

The objective of this assignment is to write modified versions of merge and quick sorts that exhibit better performance than the standard versions described in our textbook. You will implement three key improvements (one for merge sort and two for quick sort) that should improve some aspect of the algorithm's performance without requiring a great deal of additional code. You will also experimentally evaluate the impact of your improvements.

Part 1: Improved Merge Sort

Switching Strategies

The first improvement is based on the observation that merge sort is actually slower than simple O(n²) sorts for small input sizes. This may seem surprising given that merge sort is an O(n lg n) sorting algorithm. However, it is important to keep in mind that big-O analysis is only concerned with rates of growth. An O(n lg n) algorithm will always be faster than an O(n²) algorithm eventually, but that doesn't mean the O(n²) algorithm can't be faster for small inputs. The following figure was created by timing merge sort, insertion sort, and binary insertion sort on small randomly ordered lists from size 2 to size 64:

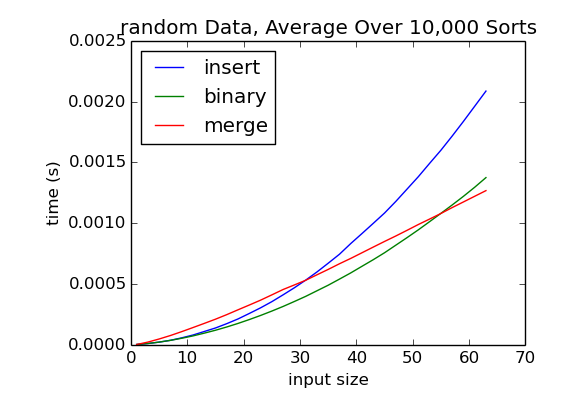
As you can see, binary insertion sort is the fastest of the three algorithms until around n = 55. At that point, merge sort becomes faster and it remains faster for all larger inputs.

A a reminder, the following pseudocode describes the overall logic of the merge sort Algorithm:

    merge_sort(sub-list)
        If sub-list is has more than one entry: 
            Recursively merge_sort the left half
            Recursively merge_sort the right half
            Merge the two sorted halves.

This logic recursively splits the original list into smaller and smaller sub-lists until the recursion bottoms out at lists of size one. This means that every time a large list is sorted, there are many recursive calls to merge sort that have small input sizes. In light of the figure above, that approach doesn't make much sense: merge sort is not a competitive sorting algorithm on small inputs. It would make more sense to recursively break the input into smaller and smaller pieces until some threshold is reached, and then switch strategies to a sorting algorithm that is more efficient on those small inputs.

The following pseudocode describes this alternate approach:

    merge_sort(sub-list)
        If sub-list is has fewer than MERGE_SORT_THRESHOLD entries:
            Sort the sub-list with binary insertion sort. 
        Otherwise: 
            Recursively merge_sort the left half
            Recursively merge_sort the right half
            Merge the two sorted halves.

Choosing an appropriate value for MERGE_SORT_THRESHOLD requires some experimentation. One of the requirements of this assignment is that you select an appropriate threshold value and provide data to justify your choice.

Finally, note that we provide an implementation of binary insertion sort that works on a full list, but you will need a version that works on a sublist for this part of the assignment. We provide a stub called binary_insertion_sort_sublist that you should implement. We do not recommend starting from scratch; copy the implementation from binary_insertion_sort and make the (relatively minor) modifications required to perform the insertion sort only on the elements of the sublist.

Part 2: Quick Sort Improvements

Median of Three Pivoting

In the textbook's version of quick sort, the last item in the sequence is always chosen as the pivot item. This is the worst possible choice for lists that are already sorted. One improvement is to examine three elements from the list and use the median of those three as the pivot. Typically, the first, middle and last items are examined. Recall that the best case for quick sort occurs when the pivot item ends up near the middle of the partitioned list and the worst case occurs when it ends up near one of the extremes. Using the median-of-three approach greatly reduces the chance that we will end up with a pivot item that is near one of the extremes. For inputs that are already sorted, the median item will be in the exact center and we will end up with best-case performance instead of worst-case.

Note that the median-of-three approach doesn't guarantee that quick sort will perform well. It is still possible to construct input sequences that will result in O(n²) comparisons.

Introspective Sort

For the large majority of inputs quick sort is very fast. There are relatively few pathological inputs that result in O(n²) performance. The idea behind introspective sort is to perform a standard quick sort until there is evidence that the current input is pathological. If it looks like the current input will cause O(n²) performance, the algorithm switches strategies to a sorting algorithm with guaranteed O(n log n) performance. Typically, heap sort is used as the alternative, since it is in-place and takes O(n log n) time in the worst case. Since we haven't yet studied heap sort, your version of introspective sort should use the improved merge sort from Part 1 as the alternate sorting algorithm. The resulting algorithm is as fast as quick sort for most inputs, but has a worst case performance of O(n log n).

It is possible to detect pathological inputs by tracking the recursion depth of the quick sort algorithm. When quick sort is working well, the partition operation typically moves the pivot item somewhere near the center of the current sub-sequence. When this is the case, the maximum recursion depth will be O(log n). Therefore, introspective sort switches strategies when the recursion depth exceeds 2 * ⌊log₂ n⌋.

Part 3: Testing and Evaluation

For this assignment you will evaluate your sorting improvements for correctness and performance. To help automate the process of testing your improvements, we have provided code (in time_sorts.py) to time the sorting algorithms and also to count the number of comparisons and assignments that occur.

Measuring clock time provides valuable data for evaluating sorting algorithms: ultimately our main concern is speed. However, there are other types of data that may provide useful insight into why one sorting algorithm exhibits better performance than another. In particular, it can be useful to count the number of comparison and assignment operations that occur during different sorting algorithms. We can accomplish this easily in Python by subclassing built-in Python data types. The following two classes are subclasses of the Python int class and list class respectively:

    class CountInt(int):
        """ A subclass of Python's built-in int class that counts the
        number of comparisons between objects of the class.

        A CountInt is exactly the same as an int, except the class-level
        variable num_comparisons is incremented during every comparison
        operation.
        """

        num_comparisons = 0
        
        def __cmp__(self, rhs):
            CountInt.num_comparisons += 1
            return super(CountInt, self).__cmp__(rhs)

        ...
        [other methods omitted]
        ...


    class CountList(list):
        """ A subclass of Python's built-in list class that counts the
        number of assignment operations performed on instances of the
        class .

        A CountList is exactly the same as a list, except the class-level
        variable num_assignments is incremented during every assignment
        operation.
        """

        num_assignments = 0

        def __setitem__(self, indx, item):
            CountList.num_assignments += 1
            super(CountList, self).__setitem__(indx, item)

In the code above, num_comparisons and num_assignments are class-level variables. This means that there is just one copy of each variable associated with the class as a whole. By overriding the comparison and assignment methods we ensure that each of those operation will be counted. In all other respects these two classes will behave exactly as the default versions would. The provided timing file (time_sorts.py) uses these classes to evaluate the performance of sorting methods on sample data sequences.

Keep in mind that your new sorting algorithms need to be correct as well as efficient. One way to test your code is to compare its output to Python's built in sorted method. For example:

    >>> a = [random.randint(0, 500) for _ in range(500)]  # Generate a random list.
    >>> b = sorted(a)                                     # Copy the list. 
    >>> sorts.insertion_sort(a)                           # Sort using my sort.
    >>> a == b                                            # Compare results.  
    True

We have included similar code in time_sorts.py that should alert you if there are correctness issues, but you may wish to do some custom testing yourself as you write the new methods for this assignment.

Submission

DEADLINE: Wednesday, November 12, 2014 at 23:59 (11:59PM) ET

You should use the python modules sorts.py and time_sorts.py as a starting point. You may make modifications to time_sorts.py for testing purposes, but you do not need to submit these modifications and you must make sure your modified sorts.py (which you WILL submit) works with the original timing code.

You must supplement the sorting algorithms provided in sorts.py with four additional algorithms:

binary_insertion_sort_sublist - This should be a modified version of binary insertion sort that sorts a sublist of the given list, from the given starting index to the given ending index.
merge_sort_switch - This should be a modified version of merge sort that switches strategies on small inputs, as described above.
quick_sort_median - Median-of-three quick sort, where the pivot item is chosen to be the median of the first, middle, and last elements in the sequence.
intro_sort - Introspective sort, where the sorting strategy is switched to the improved merge sort algorithm if the recursion depth exceeds 2 * ⌊log₂ n⌋.

Note that this PA is much like PA1 in that the amount of code that we are asking you to write is actually very small; however, completing the assignment requires that you understand a larger body of provided code and apply some theory from class as you implement the above functions. If you find yourself writing more than 50 lines of code per function, you may wish to re-evaluate your approach.

Along with your modified Python module, you must also submit a plain-text file called eval.txt that contains the output of your program on a sample execution. This file should also contain a description of the approach that you used to selecting an appropriate threshold value for switching sorting strategies in merge_sort_switch, along with the data that you used in making your decision. Finally, the file should contain a paragraph or two describing informally the general impact that your improvements made upon the performance characteristics of the sorting algorithms (total time, number of comparisons, and number of assignments). Did the performance changes match your expectations?

You should submit a zip file containing two files through the Web-CAT online submission system before the deadline: a file named sorts.py containing your completed sort modifications and a file named eval.txt containing the information described above. As always, your code should conform to the CS240 Python Coding Conventions. Make sure that the sorts.py file contains your name and the JMU Honor Code statement.

Refer to the course syllabus for the policy on late submissions. These penalties will be applied manually while grading. Web-CAT does not apply them correctly; thus, that behavior has been disabled.

CS 240

Data Structures and Algorithms - Fall 2014