PA3: Skip List Sorted Set
Introduction
The objective of this assignment is to implement a Sorted Set ADT, which is identical to the Set ADT from PA2 except that iterating over a Sorted Set produces a list of the set items in strictly increasing order. To implement the Sorted Set ADT, you will be using a variant of sorted linked lists that can perform add, remove, and search operations in expected O(log n) time by including extra list nodes and forward links to reduce the number of nodes visited while scanning the list. This structure is known as a skip list.
Part 1: Sorted Linked Lists
As a preliminary exercise, you will finish the implementation of a basic sorted linked list (a regular linked list, not a skip list), using the following file as a template:
This LinkedList class represents a sorted, singly-linked linked
list with no duplicates. Every node in the list contains a data element and a
single reference to the next node. The nodes are "sorted," in the sense that a
standard traversal of the linked list will produce a sorted sequence of all the
data elements stored in the list. The list may not contain duplicates; this
makes it appropriate for implementing a Sorted Set ADT (although the full
implementation is not part of this PA).
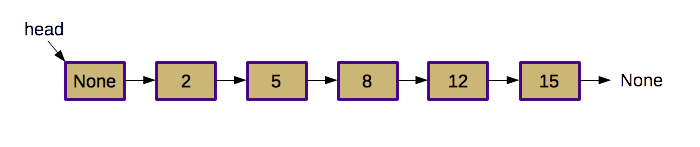
We have provided the definition of the internal Node class,
which is a simple data structure containing two public member variables:
value (the data element at the current node) and next
(the reference to the next Node object, or None if this node is the tail). We
have also provided the LinkedList constructor as well as a method
called viz(), which allows you to print a visualization of the
linked list.
This particular linked list implementation also uses a single
sentinel value at the head of the list. A sentinel value is a special
node that doesn't represent an actual object that is being stored in the list;
rather, it helps streamline the implementation of various methods by allowing
you to assume it is present rather than checking for it explicitly. For
instance, you don't need any special check for an "empty" list in the
add or remove methods, because you know there will
always be at least one node (the sentinel value) in the list.
You will implement the following methods:
add(value)- Add a value to the list, maintaining the sorted nature of the list. Thus, this method needs to scan the list to determine where the value should be inserted, and then re-arrange the references to add a newNodeobject to the list. Duplicates should not be allowed.remove(value)- Remove a value from the list, raising aKeyErrorif the value was not found in the list.__contains__(value)- This allows us to use the standard "in" keyword to test whether particular items are present in the list. This is similar to a search.__iter__(value)- This should return an iterator for the list. This will be similar to the iterator from PA2, but it should track node references rather than array indices. Because this is a sorted linked list, the elements should be returned in sorted order.
All of these methods should run in O(n) time. You should not change
the Node class, the LinkedList constructor, or the
viz() method.
Interim: Skip List Theory
One disadvantage of standard linked lists is that adding, removing, and searching in a sorted linked list is O(n). In the worst case, these operations will need to visit every node in the list, which is expensive. This makes standard sorted linked lists unattractive as the base structure of a Sorted Set ADT.
Recall that searching in a sorted array can be done in O(log n) time by exploiting the sorted nature of the array to do a binary search, eliminating half of the search space in every iteration. We would like to apply a similar technique to linked lists.
The immediate problem with doing anything similar to a binary search on standard linked lists is that you cannot access items at arbitrary indices in O(1) time (as you can in arrays). This problem can be addressed by maintaining additional information in the linked list that will allow us to "skip" large portions of the list while doing add, remove, and search operations.
The specific additional information is in the form of additional nodes, with additional links to places further along in the list. These links will allow us to selectively move forward in non-uniform intervals. Careful selection of these nodes and links will lead to expected running times of O(log n) for adding, removing, and searching. This is asymptotically faster than standard sorted linked lists.
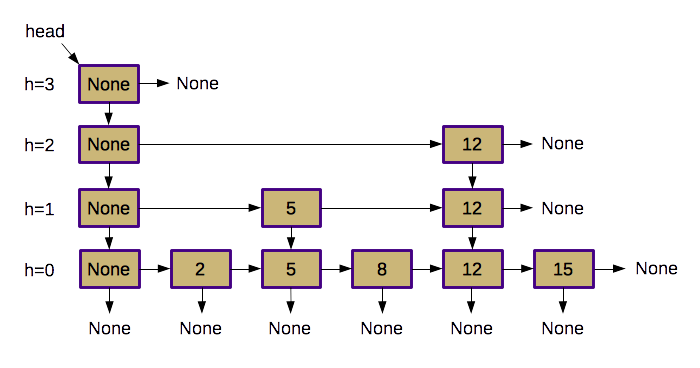
The major data structure change in a skip list is the addition of a second reference ("below") at every node. This is used to create a multi-layered structure, where the extra reference is used to link nodes vertically (just as the regular "next" reference is used to link nodes horizontally).
Observe that the bottom "layer" of a skip list is nearly identical to a standard linked list. On top of that layer, however, a skip list adds other layers of increasingly longer-distance references. Each node in the base layer may be copied into some of the higher layers when the original node is inserted. We will simulate a coin flip (50/50 chance) to determine whether a given node should be copied into the layer above it (and then another coin flip to determine whether it should be copied into the layer above it, and so forth). This will result in the height of the list being roughly log2 n layers, where n is the length of the list.
More formally, the probability that level i contains at least one node is less than n/2i, because that is the probability of i coin flips all turning up heads. This means that with high probability, the height of the skip list is O(log n). Each traversal, then, will follow no more than O(log n) downward references. It also turns out that the expected number of nodes visited on each level is O(1) because the expected number of coin flips in order to get at least one head is 2. Thus, the final expected time for a traversal is O(log n). Since all three basic operations (add, remove, search) do a constant amount of work once the desired item's location is found, the expected running time for all three operations is also O(log n).
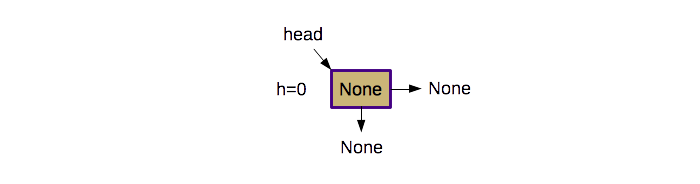
Initialization
An empty skip list consists of a single sentinel node with a value of
None and both references initialized to None. Here is
a graphical representation of an empty skip list:
Search
Searching a skip list consists of performing a traversal of the skip list. The traversal alternates between moving right ("skipping") and moving down to get closer to the desired value. If the search reaches the location in the skip list where the value should be located (i.e., the location where it would be inserted) and the value is not present, the search can conclude that the value is not in the list. Otherwise, the search will either find the value or it will reach the end of the list.
Here is pseudocode for the __contains__ method:
Initialize cur to be the head of the list.
While you haven't run off the bottom of the list:
Look for the value by advancing cur until cur.next
is None, or the cur.next.value is greater than
the value.
Move cur to the next lower level.
Return true if you found the value.
Addition
Each addition must also perform a traversal of the list; however, it is convenient to determine which layer(s) a new node should be placed in prior to traversing the list. This is because the traversal moves through the list top-to-bottom but the decision about what layer(s) the new node should be placed in is based on bottom-to-top logic: every node will always be placed in the lowest layer, and optionally copied to higher layers.
The insertion routine should simulate coin tosses to determine whether the new node should be copied to the next-highest layer. This results in tower-like structures of copied items in the list. There should be no gaps in any of these vertical towers. Because of the 50/50 nature of a coin toss, roughly half of all nodes will reside in the first layer ONLY (i.e., their first coin toss failed and they were not copied upward at all). Similarly, approximately a quarter of the nodes will reside in only the first and second layers (one succeeded coin toss, followed by a fail). Approximately an eighth of the nodes will reside in the first, second, and third layers, and this pattern continues indefinitely.
For simplicity, the single highest sentinel value is maintained on a layer of its own, and it serves as the head node of the entire list. Once the insertion routine determines the maximum height that the new node should be inserted into, it should check to see if the new node's height equals or exceeds the current height of the overall skip list. If this is the case, it should create new sentinel nodes (essentially adding new layers) until the height of the overall skip list is h+1, where h is the height of the new node.
After the list has been increased to the correct height, the insertion will add new nodes (with the new value) at any appropriate layers. This process requires a traversal of the list to determine the correct location to insert the node. The traversal begins at the head node (the highest sentinel value).
From there, the search proceeds down and to the right, testing the "next"
links to see if the value being added is greater than the value at the next
forward link. Once that condition does not hold (or if the next forward link is
None), the insertion will add the layer if the current height is
lower than or equal to the new height generated at the beginning. Then the
traversal moves to the next-lowest layer and continues.
Here is pseudocode for the add method:
Check whether the new value is already in the list; abort if found
Flip coins to determine the insertion height.
If necessary, increase sentinel height until it is one greater
than the insertion height.
Initialize cur to be the head of the list.
While you haven't run off the bottom of the list:
Find the possible insertion point at this level by advancing cur
until cur.next is None, or the cur.next.value is
greater than than the value to add.
If insertion should happen at this level:
Insert a new node after cur.
Update the below reference of the most recently added node.
Move cur to the next lower level.
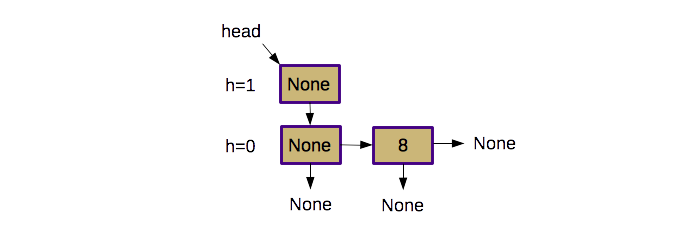
This is an example skip list after a single value has been added with a value of "8" and an insertion height of zero:
Removal
Removing an item from a skip list also requires a traversal of the list, removing a single node at each level if the value is found. Care must be taken so that no broken references remain on any levels.
Here is pseudocode for the remove method:
Initialize cur to be the head of the list.
While you haven't run off the bottom of the list:
Locate the value if it is at this level by advancing cur
until cur.next is None, or the cur.next.value is
greater than the value.
If you found the value, remove the corresponding node.
Move cur to the next lower level.
Part 2: Skip List Implementation
You will finish the implementation of a Sorted Set ADT using a sorted skip list. You may use this template to begin work:
We have provided code for the internal Node class, which is a
data structure containing three public member variables: value (the
data element at the current node) and two neighbor references: next
and below. We have also provided the SortedSet
constructor as well as a method called viz(), which allows you to
visualize the structure of your skip lists.
As with the LinkedList class, you will implement the following
methods:
add(value)- Add a value to the list as described in the section above, maintaining the sorted nature of the list. Because it is a set, the class should not allow duplicate items.remove(value)- Remove a value from the list as described in the section above, raising aKeyErrorif the value was not found in the list.__contains__(value)- Search for a value as described in the section above. This allows us to use the standard "in" keyword to test whether particular items are present in the list.__iter__(value)- This should return an iterator for the set. This will be similar to the iterator from PA2, but it should track node references rather than array indices. Because this is a Sorted Set ADT, the elements should be returned in sorted order.
Unlike the methods for LinkedList, all of the
SortedSet methods listed above (with the exception of the iterator)
should run in O(log n)
time! You should not permanently change the Node class, the
SortedSet constructor, or the viz() method.
In addition to the functions mentioned in that file, you should include implementations for all of the other functions and operators that were required in PA2. In essence, you are to provide a class that behaves identically to your Set class from PA2, except it will be much faster and the iterator will return the items in sorted order.
You should not need to re-implement all of the other Set operations using skip list traversals, however; if you did not already do this, you should be able to write them all by delegating to the implementations of the four above functions (or by delegating to each other).
There is a solution for PA2 posted on Canvas that you may use in this PA for any functions that can be written without depending on the underlying implementation. Be sure to give credit in your documentation if you use any code from the given solution.
To simulate coin tosses, you may use the following code or any code that
accurately simulates a 50/50 decision and returns a boolean:
(random.randrange(2) == 0).
Part 3: Testing
Because the interface for SortedSet is nearly identical to Set, you can use similar unit tests to the ones from PA2. However, SortedSet requires that all objects in the set be comparable. Thus, you must used a modified version of the original tests:
You may wish to add new tests to check that the iterator returns items in strictly increasing order. However, you will not be graded on your tests for this PA.
As is the case for all programming assignments in this class, part of your project grade may be based on tests that are not posted publicly. The public test cases that are run when you submit your code are provided as a courtesy to help you verify that your submission is free of syntax errors; they should not be regarded as comprehensive. You should thoroughly test your own code and code strictly to the project specification. If you have any questions about whether a particular behavior is admissible by the spec, post a question on Piazza.
Additionally, you may wish to do some performance testing to verify that your skip list implementation is faster than the linked list implementation from Part 1, or the array-based implementation of Set from PA2. Here is an example performance test:
The above test creates randomly-generated data sets and runs experiments with three different data structures: the Set from PA2 (make sure the visualization is de-activated), the LinkedList from Part 1 of this PA, and the SortedSet from Part 2 of this PA. To run the test, you will need to create a single folder with all of the following files:
linked_list.py
skip_set.py
array_set.py (from PA2)
t_array.py (from PA2)
run_comparison.py
Here is an excerpt of example output from running the performance test
(python3 run_comparison.py) on correct solutions:
...
=== 1000 ITEMS ===
<class 'array_set.Set'>
add: 0.1711 s
remove: 0.3257 s
search: 0.1655 s
<class 'linked_list.LinkedList'>
add: 0.0378 s
remove: 0.0150 s
search: 0.0226 s
<class 'skip_set.SortedSet'>
add: 0.0081 s
remove: 0.0030 s
search: 0.0040 s
...
Your results will not exactly match the numbers above, but you should check that the general trends are present. The linked list implementation should be faster than the array-based implementation; this is because performing operations in the middle of an array is more expensive than performing the same operations in the middle of a linked list. The skip list implementation should be significantly faster; this is because the base operations (add, remove, and search) can be done in O(log n) time rather than O(n).
Submission
DEADLINE: Friday, October 24, 2014 at 23:59 (11:59PM) ET
You should submit a zip file containing two .py files through the Web-CAT online submission system before the
deadline: a file named linked_list.py containing your completed
LinkedList class, and a file named skip_set.py containing your
completed SortedSet class. As always, your code should conform to the CS240 Python Coding
Conventions. Make sure that the skip_set.py file contains
your name and the JMU Honor Code statement.
Refer to the course syllabus for the policy on late submissions. These penalties will be applied manually while grading. Web-CAT does not apply them correctly; thus, that behavior has been disabled.