• A Question:
  • How would you climb to the top of a hill on a foggy night?
• One Approach:
  • Wander aimlessly until you can't take an uphill step in any direction
• Another Approach:
  • Only walk uphill
  • Don't walk too far
    
  • Stop when you can't find an uphill direction to walk in

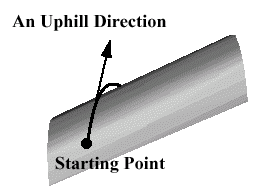
An Illustration of the Ascent Algorithm

In Pseudocode

    while (You are not at the top of the hill) {

        Find an uphill direction and face that way
        Walk as far uphill as you can in the direction you are facing
    }
    

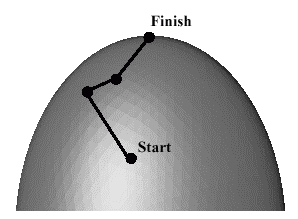
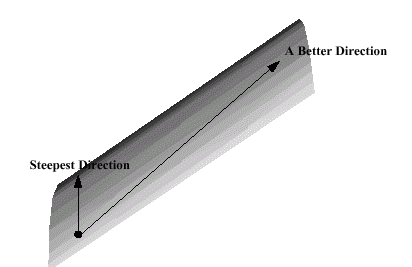
A Series of "Bad" Directions

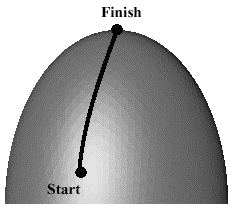
A Really Good Direction

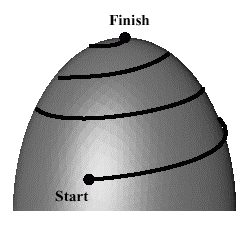
Greed is Not Always Good

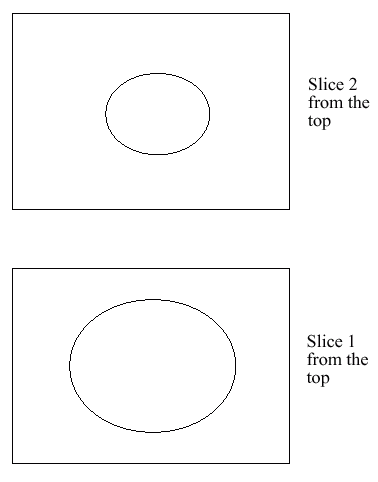
Generating Level Sets

The Level Sets for this Example

Level Sets in General

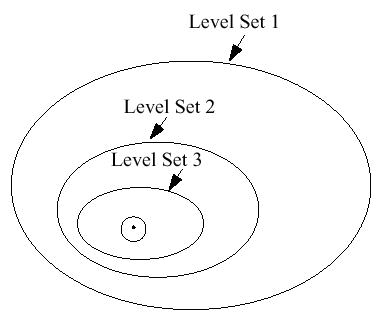
An Illustration

In Pseudocode

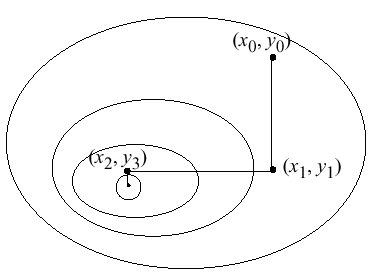
    while (You are not at the top of the hill) {

        Walk as far uphill as you can in the north/south direction
        Walk as far uphill as you can in the east/west direction
    }
    

For Minimization (NOT Maximization)

javaexamples/optimization/CyclicCoordinates.java

/**
 * The Cyclic Coordinates method for minimizing a function of one
 * variable
 *
 * @author  Prof. David Bernstein, James Madison University
 * @version 1.0
 */
public class CyclicCoordinates
{
    
    /**
     * Minimize a function
     *
     * @param f     The objective function
     * @param init  The initial solution
     * @param tol   The convergence tolerance (for the norm of x^k - x^k-1)
     * @param maxit The maximum number of iterations to perform
     * @return      The argmin over [a_0,b_0] of the function theta
     */
    public static double[] argmin(Objective f, double[] init, 
                                  double tol, int maxit)
    {
       double    change, lambda;
       double[]  y;        
       int       i, k, n;
        

       // Initialization
       k = 0;
       n = init.length;
       i = 0;

       change = tol + 1.0;
       y = new double[n];


       for (i=0; i <= n-1; i++)
       {
          f.setdi(i,0.0);
          f.setxi(i,init[i]);
          y[i] = init[i];
       }




       // Iterations
       while ((change >= tol) && (k < maxit))
       {
          k++;
          change = 0.0;
          for (i=0; i <= n-1; i++)
          {
             f.setdi(i,1.0);
             if (i >= 1) f.setdi(i-1,0.0);

             lambda = GoldenSection.argmin(f,-20.0,20.0,0.001);

             f.setxi(i,f.getxi(i) + lambda);                    
             change += lambda*lambda;
          }

          f.setdi(n-1,0.0);

          for (i=0; i <= n-1; i++)
          {
             y[i] = f.getxi(i);
          }
       }

       return y;
    }
}
        

One Approach

javaexamples/optimization/Objective.java

/**
 *  A class that is extended to create specific objective functions
 *
 *  @author  Prof. David Bernstein, James Madison University
 *  @version 1.0
 */
public abstract class Objective
{

    private  double[] d, x, y;
    private  int n;




    /**
     * Explicit Value Constructor
     *
     * @param   size The dimension of the function's domain
     */
    public Objective(int size)
    {
       n = size;
       x = new double[n];
       d = new double[n];
       y = new double[n];
    }




    
    /**
     * Evalue this function
     *
     * This method must be overriden for functions that map from R^n to R
     *
     * @param x    The n-dimensional vector argument of the function
     * @return     The function evaluated at x
     */
    public double evaluate(double[] x)
    {
       double result;
       
       
       result = 0.0;
       return result;
    }




    /**
     * Evalue this function
     *
     * This method must be overriden for functions that map from R to R
     * so that it returns the function evaluation.
     *
     * For functions that map from R^n to R it should not be overriden
     * because it will return the function evalued at x + lambda * d
     *
     * @param lambda  The 1-dimensional argument of the function
     * @return        The function evaluation
     */
    public double evaluate(double lambda)
    {
       for (int i=0; i <= n-1; i++)
       {
          y[i] = x[i] + lambda*d[i];
       }

       return evaluate(y);
    }



    /**
     * @return  The dimension of the function's domain
     */
    public int getn()
    {
       return n;
    }




    /**
     * Sets a component of the x vector
     *
     * @param i    The index to set
     * @param val  The new value of component i
     */
    public void setxi(int i, double val)
    {
       x[i] = val;
    }



    /**
     * Sets the function's x vector
     *
     * @param val  The new value of the argument
     */
    public void setx(double[] val)
    {
       for (int i=0; i <= n-1; i++)
       {
          x[i] = val[i];
       }
    }
    


    /**
     * Sets a component of the direction vector associated with this function
     *
     * @param i    The index to set
     * @param val  The new value of component i
     */
    public void setdi(int i, double val)
    {
       d[i] = val;
    }



    /**
     * Sets the direction vector associated with this function
     *
     * @param val  The new direction vector
     * @see   v11
     */
    public void setd(double[] val)
    {
       for (int i=0; i <= n-1; i++) 
       {
          d[i] = val[i];
       }
    }



    /**
     * Returns a component of the function's x vector
     *
     * @param i    The index to retrieve
     * @return     The value of component i
     * @see   v11
     */
    public double getxi(int i)
    {
       return x[i];
    }



    /**
     * Returns the function's x vector
     *
     * @return     The vector argument
     * @see   v11
     */
    public double[] getx()
    {
       return x;
    }



    /**
     * Returns a component of the direction vector associated with 
     * this function
     *
     * @param i    The index to retrieve
     * @return     component i of the direction vector
     * @see   v11
     */
    public double getdi(int i)
    {
       return d[i];
    }



    /**
     * Returns the direction vector associated with this function
     *
     * @return     The direction vector
     * @see   v11
     */
    public double[] getd()
    {
       return d;
    }




}
        

Triangulation on the Plane

An Objective Function for Triangulation on the Plane

javaexamples/optimization/TriangulationObjective.java

/**
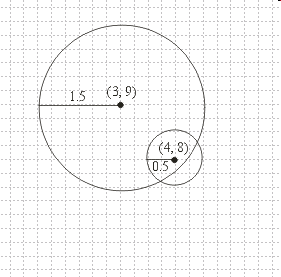
 * An objective function that illustrates the use of multidimensional
 * minimization algorithms to solve a triangulation problem
 *
 * The problem is to find the intersection of two circles.
 *
 * @author  Prof. David Bernstein, James Madison University
 * @version 1.0
 */
public class TriangulationObjective extends Objective
{

    private double[]     ci, cj;
    private double       ri, rj;
    

    /**
     * Default Constructor
     */
     public TriangulationObjective()
     {
          super(2);

          ci = new double[2];
          cj = new double[2];

          // Attributes of one circle
          ci[0] = 4.0;    // x of center
          ci[1] = 8.0;    // y of center
          ri    = 0.5;    // radius

          // Attributes of the other circle
          cj[0] = 3.0;    // x of center
          cj[1] = 9.0;    // y of center
          rj    = 1.5;    // radius
          
     }

    /**
     * Evaluate the objective function
     *
     * @param xx    A guess at an intersection point
     * @return      An indication of the extent of the error
     */
     public double evaluate(double[] xx)
     {
        double   di, dj;
        
        // The estimated radii
        di = Math.sqrt(Math.pow(ci[0]-xx[0],2.0)+Math.pow(ci[1]-xx[1],2.0));
        dj = Math.sqrt(Math.pow(cj[0]-xx[0],2.0)+Math.pow(cj[1]-xx[1],2.0));
        
        // Return the sum of the square of the differences between the
        // estimated and actual radii
        return Math.pow((di - ri),2.0)+Math.pow((dj - rj),2.0);
     }



}