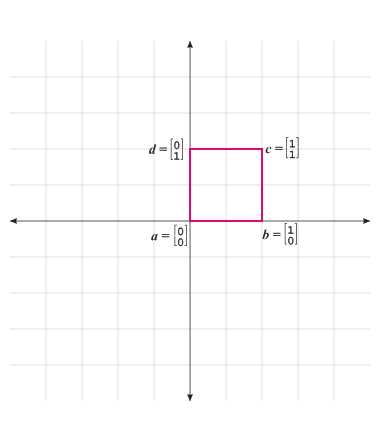
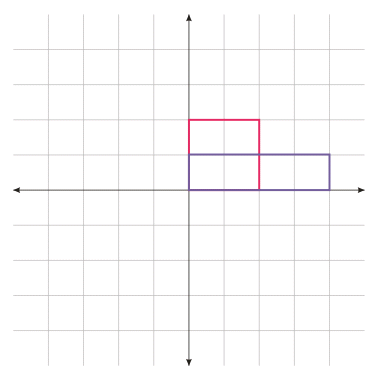
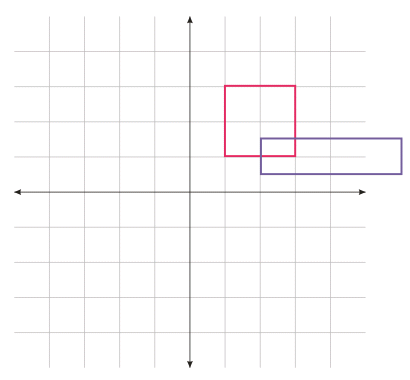
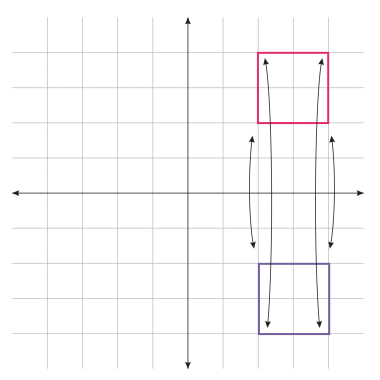
Transformation of 2D Shapes

Transformation of 2D Shapes
An Introduction

Prof. David Bernstein
James Madison University

Computer Science Department

bernstdh@jmu.edu

Motivation

What We Have:
- Methods for representing triangles and convex polygons in 2D
What We Need:
- The ability to transform these shapes in various ways

An Instructive Shape - The Unit Square

Visualization:
As a Matrix:
- \(\left[ \begin{array}{r r r r} 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1\end{array}\right]\)
- Remember that, in code, it is sometimes more convenient to use the transpose (in which each vertex is a row, not a column)

2D Transformations in General

Our Objective:
- Operate on the \(2 \times n\) matrix representation of a shape
- Get back a \(2 \times n\) matrix representation
Operations that Satisfy this Condition:
- Multiplication by a scalar
- Addition of a \(2 \times n\) matrix
- Pre-multiplication by a \(2 \times 2\) matrix

Scaling

A Uniform Scaling:
- Multiply by a scalar
Scaling Each Dimension Independently:
- Multiply by a matrix of the form \(\left[ \begin{array}{r r} \alpha & 0 \\ 0 & \beta\end{array}\right]\)

Scaling (cont.)

An Example:
- \( \left[ \begin{array}{r r} 2 & 0 \\ 0 & 0.5\end{array}\right] \left[ \begin{array}{r r r r} 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1\end{array}\right] = \left[ \begin{array}{r r r r} 0 & 2 & 2 & 0 \\ 0 & 0 & 0.5 & 0.5\end{array}\right] \)
Visualization:

Scaling (cont.)

Be Careful:
- \( \left[ \begin{array}{r r } 2 & 0 \\ 0 & 0.5\end{array}\right] \left[ \begin{array}{r r r r} 0.5 & 1.5 & 1.5 & 0.5 \\ 0.5 & 0.5 & 1.5 & 1.5\end{array}\right] = \left[ \begin{array}{r r r r} 1 & 3 & 3 & 1 \\ 0.25 & 0.25 & 0.75 & 0.75\end{array}\right] \)
Visualization:

Reflection

Around the \(x\)-Axis:
- \( \left[ \begin{array}{r r} 1 & 0 \\ 0 & -1\end{array}\right] \)
Visualization:

Reflection (cont.)

Around the \(y\)-Axis:
- \( \left[ \begin{array}{r r} -1 & 0 \\ 0 & 1\end{array}\right] \)
Visualization:

Reflection (cont.)

Around the Line \(x = -y\):
- \(\left[ \begin{array}{r r} 0 & -1 \\ -1 & 0\end{array}\right]\)
Visualization:

Reflection (cont.)

Be Careful:
- It looks like reflections do not change the area
- It looks like reflections are scalings
In Fact:
- They can change the sign of the area
- In general, reflections are not scalings (they are Householder transformations)

Shears

Along the \(x\)-Axis:
- \( \left[ \begin{array}{r r} 1 & d_{1} \\ 0 & 1\end{array}\right] \)
Visualization:

Shears (cont.)

Along the \(y\)-Axis:
- \( \left[ \begin{array}{r r} 1 & 0 \\ d_{2} & 1\end{array}\right] \)
Visualization:

Shears (cont.)

One Use of Shears:
- Italic fonts
Note:
- Shears do not change the area

Rotation

An Interesting Transformation Matrix:
- \( \left[ \begin{array}{r r} 0 & -1 \\ 1 & 0\end{array}\right] \left[ \begin{array}{r r r r} 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1\end{array}\right] = \left[ \begin{array}{r r r r} 0 & 0 & -1 & -1 \\ 0 & 1 & 1 & 0\end{array}\right] \)
Visualization:

Rotation (cont.)

Some Intuition:
What We Need:
- \( \left[ \begin{array}{r} \cos \theta \\ \sin \theta \end{array}\right] = \bs{R} \left[ \begin{array}{r r} 1 \\ 0\end{array}\right] \)
  \( \left[ \begin{array}{r} -\sin \theta \\ \cos \theta\end{array}\right] = \bs{R} \left[ \begin{array}{r}0 \\ 1\end{array}\right] \)
The Transformation Matrix that Satisfies these Conditions:
- \( \bs{R} = \left[ \begin{array}{r r} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right] \)

Rotation (cont.)

Be Careful:
- These rotations are around the origin
Note:
- Rotations do not change the area

Translation

Defined:
- Moving a shape without changing its orientation
Operation:
- Add a value to the components of each point

Combining Transformations

An Important Observation:
- Some transformations can be combined by multiplying the transformation matrixes
An Unfortunate Observation:
- Scaling, reflection, shears and rotation all involve matrix multiplication
- Translation involves vector addition

Homogeneous Coordinates

Recall:
- The homogeneous form of a line is the set of points that satisfy:
- \(h_{1}p_{1} + h_{2}p_{2} + 1 = 0\)
An Observation:
- If we add a third coordinate to each point we can write this as:
- \( \left[ \begin{array}{r} h_{1} \\ h_{2} \\ 1\end{array}\right] \cdot \left[ \begin{array}{r} p_{1} \\ p_{2} \\ 1\end{array}\right] = \left[ \begin{array}{r} 0 \\ 0 \\ 0\end{array}\right] \)
The Homogeneous Coordinate System:
- Every point \([p_{1} \quad p_{2}]\) in Cartesian coordinates corresponds to a point \([p_{1} \quad p_{2} \quad 1]\) in homogeneous coordinates

Translation in Homogeneous Coordinates

An Observation:
- \( \left[ \begin{array}{r r r} 1 & 0 & \tau_{1} \\ 0 & 1 & \tau_{2} \\ 0 & 0 & 1\end{array}\right] \left[ \begin{array}{r} p_{1} \\ p_{2} \\ 1 \end{array}\right] = \left[ \begin{array}{r} p_{1}+\tau_{1} \\ p_{2}+\tau_{2} \\ 1 \end{array}\right] \)
Interpretation:
- In homogeneous coordinates, we can translate a point using matrix multiplication

Translation in Homogeneous Coordinates (cont.)

Translation Matrix:
- \( \bs{T} = \left[ \begin{array}{r r r} 1 & 0 & \tau_{1} \\ 0 & 1 & \tau_{2} \\ 0 & 0 & 1\end{array}\right] \)
Inverse Translation Matrix:
- \( \bs{T}^{-1} = \left[ \begin{array}{r r r} 1 & 0 & -\tau_{1} \\ 0 & 1 & -\tau_{2} \\ 0 & 0 & 1\end{array}\right] \)

Scaling in Homogeneous Coordinates

Scaling Matrix:
- \( \bs{S} = \left[ \begin{array}{r r r} \sigma_{1} & 0 & 0 \\ 0 & \sigma_{2} & 0 \\ 0 & 0 & 1\end{array}\right] \)
Inverse Scaling Matrix:
- \( \bs{S}^{-1} = \left[ \begin{array}{r r r} 1 / \sigma_{1} & 0 & 0 \\ 0 & 1/ \sigma_{2} & 0 \\ 0 & 0 & 1\end{array}\right] \)

Shears in Homogeneous Coordinates

Along the \(x\)-Axis:
- \( \left[ \begin{array}{r r r} 1 & d_{1} & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right] \)
Along the \(y\)-Axis:
- \( \left[ \begin{array}{r r r} 1 & 0 & 0 \\ d_{2} & 1 & 0 \\ 0 & 0 & 1\end{array}\right] \)

Rotation in Homogeneous Coordinates

Rotation Matrix (Around the Origin):
- \( \bs{R} = \left[ \begin{array}{r r r} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{array}\right] \)
Inverse Rotation Matrix:
- Use the negative of the angle

Rotation in Homogeneous Coordinates (cont.)

Rotation Around a Point:
- Translate the center of rotation to the origin, rotate, translate back
The Result:
- \( \left[ \begin{array}{r r r} 1 & 0 & -x \\ 0 & 1 & -y \\ 0 & 0 & 1\end{array}\right] \left[ \begin{array}{r r r} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{array}\right] \left[ \begin{array}{r r r} 1 & 0 & x \\ 0 & 1 & y \\ 0 & 0 & 1\end{array}\right] = \left[ \begin{array}{r r r} \cos \theta & -\sin \theta & -x(\cos \theta -1) + y \sin \theta \\ \sin \theta & \cos \theta & -x \sin \theta - y(\cos \theta -1) \\ 0 & 0 & 1\end{array}\right] \)

Reflection in Homogeneous Coordinates

Around the \(x\)-Axis:
- \( \left[ \begin{array}{r r r} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1\end{array}\right] \)
Around the \(y\)-Axis:
- \( \left[ \begin{array}{r r r} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right] \)

Combining Transformations in Homogeneous Coordinates

An Important Observation:
- Different transformations can be combined by multiplying the transformation matrixes
Efficiency:
- It is generally more efficient to combine the transformations

There's Always More to Learn