The Time Value of Money

The Time Value of Money
An Introduction

Prof. David Bernstein
James Madison University

Computer Science Department

bernstdh@jmu.edu

Motivation

A Question:
- Would you rather I give you $100 today or $100 in ten years (guaranteed)?
Why?
- This is the key to understanding the time value of money

Interest

Consider a Simple Savings Account:
- When you deposit money in a savings account it accrues interest (i.e., the bank will allow you to withdraw more than you deposited)
An Example:
- How much will you be able to withdraw in a year if the annual interest rate is 5%?

A Formalization

Notation:
- $P$ denotes the present value (e.g., the initial deposit in your account)
- $n$ denotes the year
- $F_n$ denotes the future value in year $n$ (e.g., the balance in your account in year $n$)
- $I$ denotes the interest earned
- $r$ denotes the interest rate per year
Simple Interest:
- Interest is earned only on the initial deposit
- $I = P \cdot n \cdot r$
An Example:
- $P = 100$
- $r = 0.10$
- $n = 1$
- So, $I = 100 \cdot 1 \cdot 0.10 = 10$

A Formalization (cont.)

Compound Interest:
- Interest is earned on both the initial deposit and the prior interest
An Example (with the same values as above):
- Interest in Year 1: $100 \cdot 0.10 = 10.00$
- Interest in Year 2: $110 \cdot 0.10 = 11.00$
- Interest in Year 3: $121 \cdot 0.10 = 12.10$
The Recurrence Relation:
- $F_0 = P$
- $F_1 = F_0 + F_0 \cdot r = F_0 \cdot (1 + r) = P\cdot(1 + r)$
- $F_2 = F_1 + F_1 \cdot r = F_1 \cdot (1 + r) = P\cdot(1 + r)\cdot(1 + r) = P \cdot (1+r)^2$
- $F_3 = F_2 + F_2 \cdot r = F_2 \cdot (1 + r) = P \cdot(1 + r)^3$
- $\vdots$
- $F_n = F_{n-1} + F_{n-1} \cdot r = F_{n-1} \cdot (1 + r) = P \cdot (1+r)^n$

A Modified Version of the Original Question

Suppose:
- The interest rate is (and will continue to be) 10%
Which Would Your Prefer?
- $100 today
- $110 in one year
- $121 in two years

Calculating the Present Value

Suppose you are Given:
- The interest rate: $r$
- The year: $n$
- The future value in year $n$: $F_n$
The Present Value:
- $P = \frac{F_n}{(1+r)^n}$
An Example:
- $n = 6$
- $F_n = 1000$
- $r = 0.08$
- $P = \frac{1000}{1.08^6} = \frac{1000}{1.59} = 630.17$

An Example

Setting:
- Your company has been approached to develop and maintain a software product
- You are going to receive revenues, $R$, over time
- You are going to incur costs, $C$, over time
The Proposed Contract:

An Example (cont.)

The Interest Rate:
- Your company can borrow money at 4% (i.e., $r = 0.04$)
Summary of the Calculations:

An Example (cont.)

Discounting the Revenue Stream

An Example (cont.)

Discounting the Cost Stream

An Example (cont.)

An Alternative Approach - Discounting the Profit Stream

Annuities

Defined:
- The same amount of money, $A$, is "received" each year
Given What We Already Know:
- $P = \frac{A}{(1+r)^1} + \frac{A}{(1+r)^2} + \cdots + \frac{A}{(1+r)^{(n-1)}} + \frac{A}{(1+r)^n} $

Annuities (cont.)

Simplifying:
- $P = A \left[\frac{1}{(1+r)^1} + \frac{1}{(1+r)^2} + \cdots + \frac{1}{(1+r)^{(n-1)}} + \frac{1}{(1+r)^n}\right] $
This Can be Reduced To:
- $P = A \left[ \frac{1-(1+r)^{-n}}{r}\right] $

Annuities (cont.)

In General:
- $F_n = P (1 + r)^n$
For an Annuity:
- $F_n = A \left[ \frac{1-(1+r)^{-n}}{r}\right] (1 + r)^n$
This can be Simplified To:
- $F_n = A \left[ \frac{(1+r)^{n} - 1}{r}\right]$

Annuities (cont.)

Suppose:
- I deposit 1000 per year for 10 years at 0.05
- $F_{10} = 1000 \left[ \frac{1.05^{10} - 1}{0.05}\right] = 1000 \left[ \frac{1.63 - 1}{0.05}\right] = 12577.89$
Suppose:
- I'm graduating from college and want to have $1,000,000 in 30 years and the interest rate is 0.08
- $1000000 = A \left[ \frac{1.08^{30} - 1}{0.08}\right] = A \cdot 113.28$
- So, I need to deposit 1,000,000/113.28 = $8,827.68 every year

Internal Rate of Return

In Some Situations:
- We know the present value and a stream of cash flows (over a given number of years) and we want to find the interest rate that makes us indifferent between the two
An Example:
- I can invest a given amount of money in a project now
- If I do, I am guaranteed a stream of payments in the future

Internal rate of Return (cont.)

One Way To Proceed (or Maybe Not):
- Write a program that tries every possible interest rate

A Better Way To Proceed - Bisection:


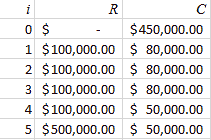
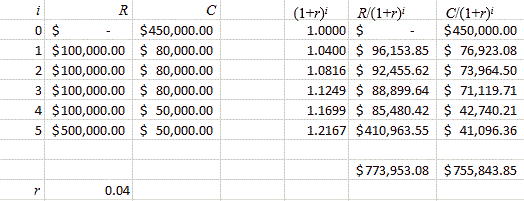
                              low   = a lower bound
   high  = an upper bound
   
   while (high and low are too far apart)
   {
      guess = (low + high) / 2.0

      calculate the PV for flow using guess

      if (PV > 0.0)         // guess is too low
      {
         low  = guess;         
      }
      else if (PV < 0.0) // guess is too high
      {
         high = guess;
      }
      else                  // guess is just right
      {
         low = high = guess;
      }
   }

   return (low + high)/2.0

There's Always More to Learn