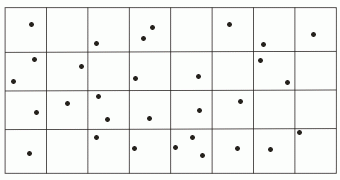
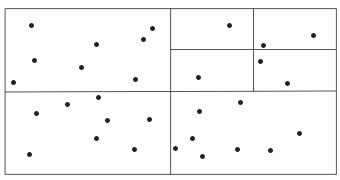
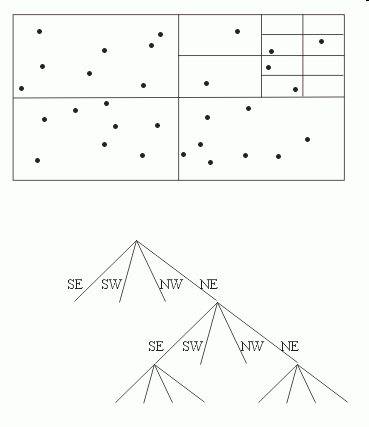
Partitioning Spatial Data

Partitioning Spatial Data
An Introduction

Computer Science Department

bernstdh@jmu.edu

Motivation

A Problem:
- Find the characteristics of a point feature at a particular location
Our Concern:
- What data structures and algorithms can and should be used?

Review

A Similar Problem You've Seen Before:
- Find the characteristics of an element in a collection
Approaches That Use Contiguous Memory:
- Use the element ID as the index
- Don't sort and use linear search
- Sort and use binary search
Approaches That Use Linked Memory:
- Linear structure, don't sort, use linear search
- Linear structure, sort, use binary search
- Binary tree structure, fully or partially sorted
- Hashtable

Review (cont.)

How You Evaluated These Approaches:
1. Determined the necessary operations
2. Determined the efficiency of the different operations
How You Determined The Efficiency:
- Considered worst cases
- Used asymptotic comparisons

Returning the Original Problem

Finding a Point

A "Classical" Approach:
- Contiguous or linked memory
- Don't sort the elements
- Use linear search
Issues:
- Only the obvious (i.e., performance, fixed size, etc...)

Finding a Point (cont.)

Another "Classical" Approach:
- Contiguous or linked memory
- Use the element "ID" as the index
Issues:
- The "ID" consists of two coordinates. Can a single ID be created?

Finding a Point (cont.)

A Third "Classical" Approach:
- Contiguous or linked memory
- Sort based on the "ID"
- Use binary search
Issues:
- Theres is no "natural" way to order points that consists of two coordinates.

Finding a Point (cont.)

A "New" Approach:
- Divide the plane into a grid with equally sized cells
- Put each cell in a two-dimensional array
- Each cell contains 0 or more points, unordered, in a linear structure
Analysis:
- $O(1)$ to find the appropriate cell
- $O(n)$ to find a point in a cell (because one cell might contain all of the points

Finding a Point (cont.)

Another "New" Approach:
- Divide the plane into quarters then iteratively divide each cell that contains more than one point into quarters
The Initial Partition:
The Second Partition:

Finding a Point (cont.)

Finding a Point (cont.)

A Data Structure for this Approach:
- Use a linked tree structure
- Each node is either a leaf or has 4 children (NE, NW, SW, SE)
Finishing the Initial Northeast Cell:

Finding a Point (cont.)

Conceptually:
- Like a binary tree
- We can't use just horizontal or just vertical partitioning since points can be on a horizontal or vertical line
Analysis:
- $O(\log n)$ to find a point

There's Always More to Learn