• A Quiz:
  • Are you smarter than the average person?
• From Our Study of Statistical Inference:
  • If "you" is plural (i.e., refers to the entire class) then we can make use of the sample mean and standard deviation and conduct a \(t\) test
• Today's Question:
  • Why are you so smart?

• Francis Galton's Original (1886) Usage:
  • Average height of sons of tall fathers was less than the height of the fathers
  • Average height of sons of short fathers was more than the height of the fathers
  • Tall and short sons regress towards the average
  • The article - "Regression towards Mediocrity in Hereditary Stature"
• An Example of Modern Usage:
  • How does the average height of sons depend on the height of their fathers?

• Defined:
  • Study of the dependence of one variable (called the endogenous or dependent variable) on one or more other variables (called the exogenous or independent or explanatory variables)
• Be Careful:
  • It identifies a statistical dependence not causation
• Relation to the Discipline of Statistics:
  • Statistical estimation determines model parameters based on empirical data
  • Regression analysis is a statistical estimation technique

• Notation:
  • \(X\) denotes the explanatory variable
  • \(Y\) denotes the dependent variable
• The Model:
  • \(Y = f(X)\)

• Models that are Linear in Parameters:
  • \(Y = \alpha + \beta X\)
• The Parameters to Estimate:
  • \(\alpha\) and \(\beta\)
• An Important Observation:
  • The model is linear in the parameters. So, the explanatory variable can be anything (e.g., it can be income-squared, it can involve logarithms, etc...)

• What We Collect:
  • Observations of \(X\) and corresponding observations of \(Y\)
• Notation:
  • \(X_i\) denotes the \(i\)th observation of the explanatory variable
  • \(Y_i\) denotes the corresponding \(i\)th observation of the dependent variable

• Exactly One Observation, \((Y_1, X_1)\):
  • Since it takes two points to define a line, we can't estimate both \(a\) and \(b\)
• Exactly Two Observations, \((Y_1, X_1)\) and \((Y_2, X_2)\)
  • We have two equations and two unknowns (so can find both \(\alpha\) and \(\beta\)) but not enough data to find statistically significant results

• A Perfect Fit:
  • We have many observations and they are all on a single line
• Why this is Unlikely:
  • The theory/model is unlikely to be perfect
  • It is difficult to measure some variables
  • Intrinsic randomness in the dependent variable

• A Typical Scatter Plot:
  • 
• Mathematical Representation:
  • \(Y_i = \alpha + \beta X_i + \epsilon_i \; \; \; i = 1, \ldots, n\)

• In General:
  • Choose the "best" line (i.e., find the values of \(\alpha\) and \(\beta\) that give the "best" fit)
• Least Absolute Deviation:
  • \[\min \sum_{i=1}^{n} | \epsilon_i |\]
• Least Squared Deviation:
  • \[\min \sum_{i=1}^{n} \epsilon_i^2\]

• An Observation:
  • Both have good properties
  • Both can be solved numerically
• An Advantage of Least Squares:
  • We can solve for \(\alpha\) and \(\beta\) in closed form using calculus

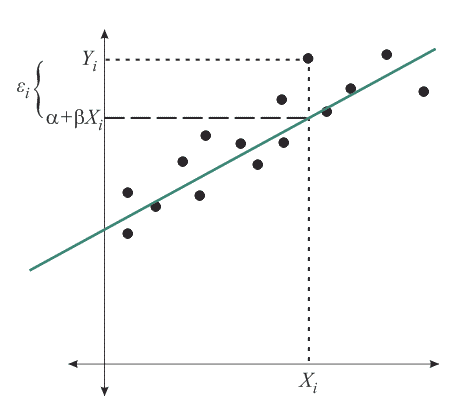
For linear models through the origin (i.e., with just \(\beta\)) we have:

\[ \min \sum_{i=1}^n (Y_i - \beta X_i)^2 = (Y_1 - \beta X_1)^2 + \cdots + (Y_n - \beta X_n)^2 \]

which we need to differentiate, set to 0, and solve.

\[ \frac{d}{d \beta} \sum_{i=1}^{n}(Y_i - \beta X_i)^2 = \frac{d (Y_1 - \beta X_1)^2}{d\beta} + \cdots + \frac{d (Y_n - \beta X_n)^2}{d\beta} \] \[ = 2\cdot-X_1\cdot(Y_1 - \beta X_1) + \cdots + 2 \cdot -X_n \cdot (Y_n - \beta X_n) \] \[ = 2 \sum_{i=1}{n} -X_i \cdot (Y_i - \beta X_i) = 2 \sum_{i=1}^{n} -X_i Y_i + 2 \sum_{i=1}^{n} \beta X_i^2 \]

So, at the minimum:

\[ \sum_{i=1}^n X_i Y_i = \sum_{i=1}^n X_i^2 \]

which implies that, at the minimum, \(\beta = \frac{\sum_{i=1}^n X_i Y_i}{\sum_{i=1}^n X_i^2}\)

For affine models (i.e., with both \(\alpha\) and \(\beta\)) we need to take partial derivatives, set them equal to 0, and solve.

Starting with \(\alpha\):

\[ \frac{\partial}{\partial \alpha} \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i)^2 = 2 \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i) \cdot -1 \] At the minimum: \[ \sum_{i=1}^{n}Y_i - \sum_{i=1}^{n} \alpha - \sum_{i=1}^{n} \beta X_i = 0 \Rightarrow n \cdot \alpha = \sum_{i=1}^{n}Y_i - \beta \sum_{i=1}^{n}X_i \] Dividing by \(n\): \[ \alpha = \overline{Y} - \beta \overline{X} \] where \(\overline{Y}\) and \(\overline{X}\) are the mean of \(Y\) and \(X\) respectively.

Now solving for \(\beta\):

\[ \frac{\partial}{\partial \beta} \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i)^2 = 2 \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i) \cdot -X_i \] At the minimum: \[ \sum_{i=1}^{n}Y_i X_i - \sum_{i=1}^{n}\alpha X_i - \sum_{i=1}^{n} \beta X_i^2 = 0 \Rightarrow \sum_{i=1}^{n}Y_i X_i - \alpha \sum_{i=1}^{n} X_i - \beta \sum_{i=1}^{n}X_i^2 = 0 \] Substituting \(\alpha = \overline{Y} - \beta \overline{X}\) \[ \sum_{i=1}^{n}Y_i X_i - \overline{Y} \sum_{i=1}^{n} X_i + \beta \overline{X} \sum_{i=1}^{n} X_i - \beta \sum_{i=1}^{n}X_i^2 = 0 \] which implies \[ \sum_{i=1}^{n}X_i(Y_i - \overline{Y}) + \beta \sum_{i=1}^{n} X_i (\overline{X} - X_i) = 0 \] Solving for \(\beta\): \[ \beta = \frac{\sum_{i=1}^{n}X_i(Y_i - \overline{Y})}{\sum_{i=1}^{n} X_i (X_i - \overline{X})} \]

• Errors in the Process:
  • The model is a simplification of reality
  • There is error in the collection and measurement of the data
• The Implications:
  • Each observation of \(Y\) (i.e., each \(Y_i\)) is a random variable
  • We should think about the properties of \(\epsilon\) and what this means for the model \(Y_i = \alpha + \beta X_i + \epsilon_i\)

• Assumptions:
  • The error term has zero expected value [i.e., \(E(\epsilon_i)=0\)], and constant variance [i.e., \(E(\epsilon_i^2)=\sigma^2\)]
  • The random variables \(\epsilon_i\) are uncorrelated
• Implications for OLS Estimators:
  • \(\text{Var}(\beta) = \frac{\sigma^2}{\sum(X_i - \overline{X})^2}\)
  • \(\text{Var}(\alpha) = \sigma^2 \left[ \frac{\sum X_i^2} {n \sum(X_i - \overline{X})^2} \right]\)

• We Can Estimate \(\sigma^2\):
  • \(s^2 = \frac{\epsilon_i^2}{n-2}\)
• We Can Test Hypotheses:
  • Using \(s^2\) in place of \(\sigma^2\) we can determine whether \(\alpha\) and \(\beta\) are significantly different from 0

• A Question:
  • What can we do if there are multiple explanatory variables?
• The Answer:
  • We can do the same kind of thing for models of the form:
  • \(Y_i = \alpha + \beta_1 X_{1i} + \beta_2 X_{2i} + \cdots + \beta_k X_{ki} + \epsilon_i\)
  • where \(X_{1}\) denotes the first independent variable and \(X_{1i}\) denotes the \(i\)th observation of the first independent variable, etc...

• Percentage of the Total Variation that is Explained:
  • \[ R^2 = 1 - \frac{\sum_{i=1}^{n}\epsilon_i^2}{\sum_{i=1}^{n}(Y_i - \overline{Y})^2} \]
• Correcting for the Number of Explanatory Variables (\(k\)):
  • \[ \overline{R}^2 = 1 - \frac{\sum_{i=1}^{n}\epsilon_i^2/(n-k)}{\sum_{i=1}^{n}(Y_i - \overline{Y})^2/(n-1)} \]