

|
Queueing Theory
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
Queueing Theory
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |







 : Modeling State Transitions in Queues
: Modeling State Transitions in Queues

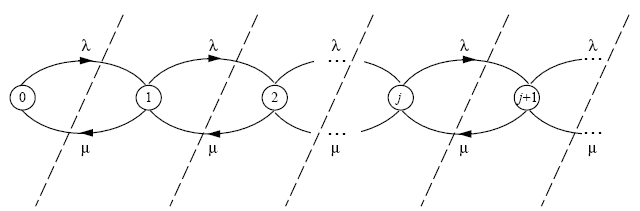
 : Modeling Steady States in Queues
: Modeling Steady States in Queues

 : Modeling Steady States in Queues
: Modeling Steady States in Queues

 : Modeling Steady States in Queues (cont.)
: Modeling Steady States in Queues (cont.)

 : Modeling Steady States in Queues (cont.)
: Modeling Steady States in Queues (cont.)

 : Modeling Steady States in Queues (cont.)
: Modeling Steady States in Queues (cont.)








