• Early Technologies:
  • It is believed that the Phoenicians (600 BC) knew how to measure latitude
  • The Greeks (325 BC) used a gnomon to measure the height of the sun above the horizon and the time of the year to measure latitude
• More Recent Technologies:
  • Astrolabe (1400s)
  • Backstaff (1500s)
  • Quadrant (1600s)
  • Octant (1600s)
  • Sextant (Newton and Hadley in the 1700s)

• Getting Started:
  • Orient the crossbar (using a compass) so that it points North-South
• Taking the Measurement:
  • Align the sights with Polaris
  • Read the angle of the plumb bob on the protractor

• Light from Infinity:
  • As the distance to a light source approaches infinity, the rays from that source approach being parallel
• Position of Polaris:
  • Polaris is above the North Pole (which is why it is often called the North Star)

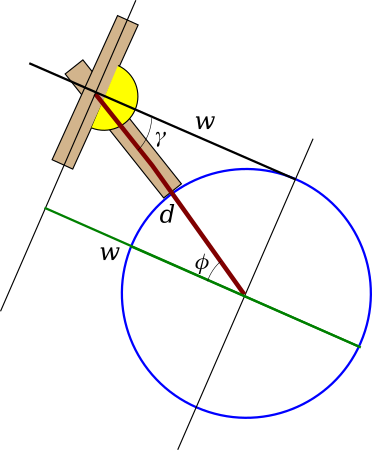
The latitude of the quadrant (which is what we are trying to measure) is denoted by \(\phi\).

The plumb bob points to the center of the Earth.

\(\cos(\gamma) = \frac{w}{d}\) and \(\cos(\phi) = \frac{w}{d}\) imply that \(\cos(\gamma) = \cos(\phi) \Rightarrow \gamma = \phi\)

• Purpose:
  • Measure the elevation (above the horizon) of a distant object
• An Example:
  • 

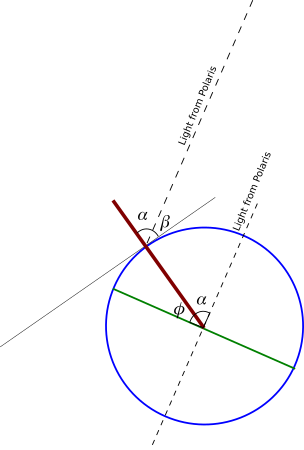
The latitude of the observer (which is what we are trying to measure) is denoted by \(\phi\).

Because the light rays are parallel, the angle they form with the red line is the same and denoted by \(\alpha\).

The measured angle of elevation is \(\beta\).

\(\alpha + \phi = 90\) and \(\alpha + \beta = 90\) imply that \(\alpha + \phi = \alpha + \beta \Rightarrow \phi = \beta\),