Heaps

Heaps
An Introduction

Computer Science Department

bernstdh@jmu.edu

Motivation

A Definition:
- A "normal" d-heap is a tree with the property that a parent's "value" is not smaller than the "value" of any of its \(d\) children
- An "inverted" heap is ordered the other way.
Applications:
- Priority Queue (i.e., a queue in which the elements are ordered based on their "priority" not their "arrival time"
- Sorting

An Example

A 3-Heap

Creating and Maintaining a Heap

Sift Down - move an element that is not properly positioned down the tree (i.e., towards its descendants)
Sift Up - move an element that is not properly positioned up the tree (i.e., towards the root)

The "Sift Up" Process

siftup(i) { while (i is not the root node and i.value > i.parent.value) { swap(i, i.parent); } }

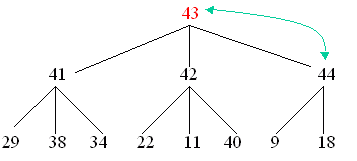
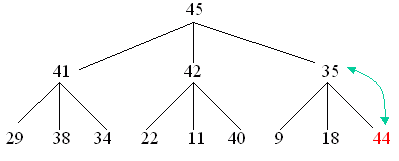
Suppose a node with value 44 is added to the end of the 3-heap above...

The "Sift Down" Process

siftdown(i) { while (i is not a leaf node and i.value < i.maxchild.value) { swap(i, i.maxchild); } }

Suppose the value of the root node is changed to 43...

Adding and Removing Nodes

add(i) { add i to the back of the heap; siftup(i); }

remove() { swap(front, back); remove the back element; siftdown(front); }

Time Efficiency Bounds

Sift Down and Sift Up:
- \(O(\log n)\)
Add:
- \(O(1)\) to add to the back
- \(O(\log n)\) to sift up
Remove:
- \(O(1)\) to swap
- \(O(1)\) to remove from the back
- \(O(\log n)\) to sift down

There's Always More to Learn