Great Circle Distances

Great Circle Distances
for a Spherical Planet

Computer Science Department

bernstdh@jmu.edu

Definitions

Great Circle:
- A section of a sphere that contains a diameter of the sphere
Orthodrome:
- Shortest distance between points on a sphere (which will be a segment of a great circle)

From Longitude/Latitude to Cartesian Coordinates

Notation

From Longitude/Latitude to Cartesian Coordinates (cont.)

Derivation of the Conversion:
- $\cos \phi = d / R \Rightarrow d = R \cos \phi$
- $\cos \lambda = p_{z}/d \Rightarrow p_{z} = d \cos \lambda = R\cos \phi \cos \lambda$
- $\sin \lambda = p_{x}/d \Rightarrow p_{x} = d \sin \lambda = R \cos \phi \sin \lambda$
- $p_{y} = R \sin \phi$
Note:
- This is very similar to the conversion of spherical coordinates to Cartesian coordinates (but uses the latitude not the colatitude)

Finding the Great Circle Distance

The great circle distance is the portion of the circumference described by $\alpha$ .

Arc Length (Using Degrees):
- $d = \frac{\alpha}{360} \cdot 2 \pi R$
Arc Length (Using Radians):
- $d = \frac{\alpha}{2 \pi} \cdot 2 \pi R = \alpha R$

Going Further

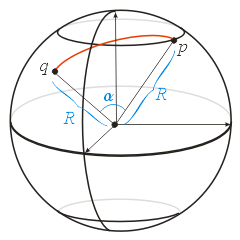
: Finding the Angle from the Longitude and Latitude

From the Law of Cosines:
- $\cos \alpha = \frac{\bs{q} \cdot \bs{p}}{||\bs{q}|| \enspace ||\bs{p}||}$
Solving:
- $\cos \alpha = \frac{ (R \cos \phi_{q} \cos \lambda_{q}) (R \cos \phi_{p} \cos \lambda_{p}) + (R \cos \phi_{q} \sin \lambda_{q}) (R \cos \phi_{p} \sin \lambda_{p}) + (R \sin \phi_{q})(R \sin \phi_{p}) }{R R}$
- $\alpha = \cos^{-1} (\cos \phi_{q} \cos \lambda_{q}) (\cos \phi_{p} \cos \lambda_{p}) + (\cos \phi_{q} \sin \lambda_{q}) (\cos \phi_{p} \sin \lambda_{p}) + (\sin \phi_{q})(\sin \phi_{p})$

There's Always More to Learn