|
State Models
with UML |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
State Models
with UML |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |





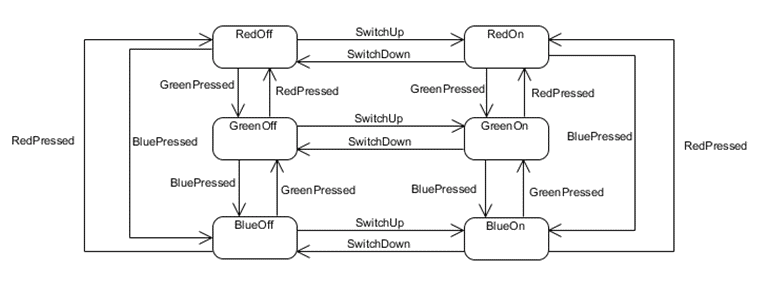
power
T (i.e., On)F (i.e., Off)







color,
and one boolean attribute, power
power, color) where power
can take on the values T and F, and
color can take on the values R,
G, and B
(T, R), (T, G), (T, B), (F, R), (F, G), (F, B)}













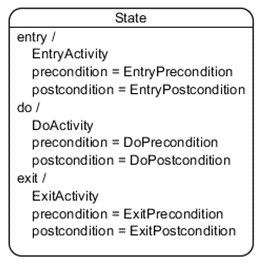



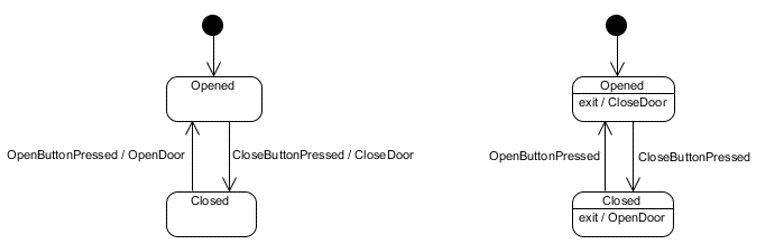
In general, one should use an entry action when the behavior should be executed regardless of how the state is entered. On the other hand, one should use an effect when the behavior is specific to the transition.


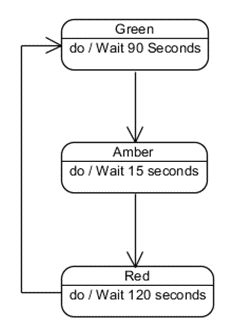






An Example
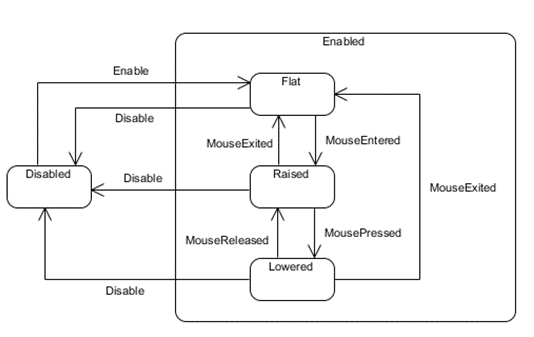
In the abstract model, this system has two states, Disabled and Enabled, and transitions between the two as a result of two events, Enable and Disable.






Example
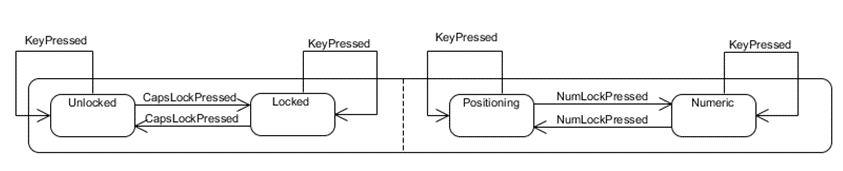
Note that, because of the orthogonal regions, we do not have to define the states UnlockedPositioning, LockedPositioning, UnlockedNumeric, and UnlockedArrows.






color,and
one boolean attribute, power