|
The Representation of Data
An Overview |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
The Representation of Data
An Overview |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |











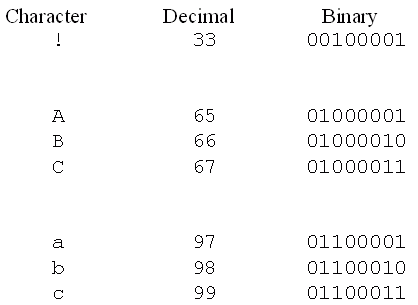
 : What About Real Numbers? (cont.)
: What About Real Numbers? (cont.)

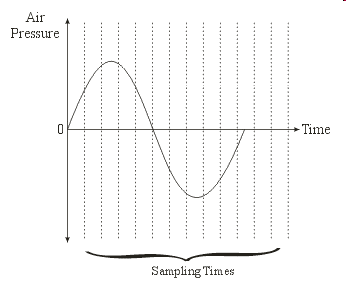
 : What About Real Numbers? (cont.)
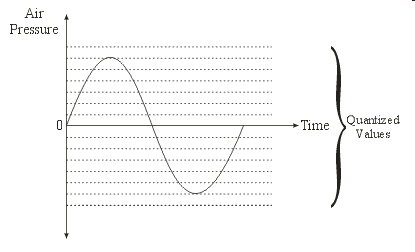
: What About Real Numbers? (cont.)