- Forward


Binary Search Trees
An Introduction


Prof. David Bernstein
James Madison University

Computer Science Department
bernstdh@jmu.edu

Print

Background
Back SMYC Forward
  • Tree:
    • A connected graph with no circuits
  • Binary Search Tree:
    • A binary tree in which each node contains a larger value than all the values in its left subtree and a smaller value that all the values in its right subtree
  • Balanced Binary Search Tree:
    • A roughly symmetrical BST
    • One common definition is that there is a difference of at most one level of depth among the various leaves
An Example
Back SMYC Forward

Using a Linked Structure

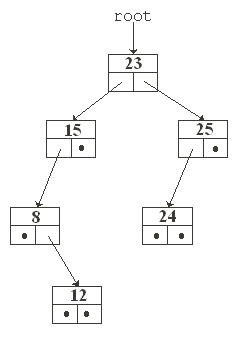
linked_bst

Traversals

A preorder traversal of this BST will print the values in the nodes in the following order: 23, 15, 8, 12, 25, 24

A postorder traversal of this BST will print the values in the nodes in the following order: 12, 8, 15, 24, 25, 23

Searching with BSTs
Back SMYC Forward

A Recursive Algorithm

  • The Easy Case(s):
    • The Node is empty
    • The Node contains the target
  • Refinement:
    • Search either the left or right child
search(current, target) { if (current == null) print("Not present!") else if (current's data == target) print("Found!") else if (current's data >target) search(current's left, target) else search(current's right, target) }
Searching with BSTs (cont.)
Back SMYC Forward

A Non-Recursive Algorithm

search(current, target { while ( (current != null) && (current's data != target) ) { if (current's data > target) current = current's left else current = current's right } if (current's data == target) print("Found!") else print("Not present!") }
Sorting with BSTs
Back SMYC Forward
  • An Example:
    • linked_bst
  • Sorting with Inorder Traversal:
    • An inorder traversal visits the nodes in the following order: 8, 12, 15, 23, 24, 25
Inserting Nodes into a BST
Back SMYC Forward
  • The Easy Case:
    • If the tree is empty, make root the new node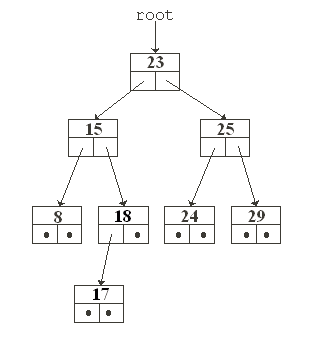
  • Refining the Other Cases:
    • If the tree is not empty and the new node is less than the existing node, insert the new node into the left subtree
    • If the tree is not empty and the new node is greater than the existing node, insert the new node into the right subtree
  • An Example:
    • bst_add_remove
    • A 21 would be inserted as the right child of the node containing the 18
    • A 26 would be inserted as the left child of the node containing the 29
Inserting Nodes into a BST (cont.)
Back SMYC Forward

Ignoring Balance

insert(current, n) { if (current == null) current = n; else if (n's data < current's data) insert(current's left, n) else if (n's data > current's data) insert(current's right, n) else print("Duplicate!") }
Removing Nodes from a BST
Back SMYC Forward
  • The Easy Cases:
    • If the node to be removed is a leaf then it must be replaced by null
    • If the node to be removed has one nonempty subtree then the parent of the node to be removed must be adjusted to point to the nonempty subtree
  • The Hard Case - A Node with Two Nonempty Subtrees:
    • We must decide which subtree should be pointed to by the parent
    • There are several ways to do this
Removing Nodes from a BST (cont.)
Back SMYC Forward
  • One Way to Handle the Hard Case:
    • Find the "immediate predecessor" of the node being removed by moving to its left child and then as far right as possible
    • Remove immediate predecessor
    • Replace the removed node with the immediate predecessor
  • Why It Works:
    • The immediate predecessor has no right child (since we went as far right as possible)
    • So, it can be easily removed from its current position
Removing Nodes from a BST (cont.)
Back SMYC Forward
  • An Example:
    • bst_add_remove
  • The Node to Remove:
    • The root node
  • The Process:
    • Move to its left child and search to the right as far as we can which gets us to the node containing the 18
    • Remove that node (using the algorithm discussed above)
    • Replace the value in the root node with the 18
  • The Resulting BST:
    • bst_after_remove
There's Always More to Learn
Back -