| (1) |
_____
|
The degree (or valency) of a vertex is: |
|
||
| (2) |
_____
|
A graph which contains no circuits is said to be: |
|
||
| (3) |
_____
|
A label correcting algorithm for finding shortest paths: |
|
||
| (4) |
_____
|
A "great circle" is: |
|
||
| (5) |
_____
|
Which of the following is a type of automatic vehicle location system? |
|
||
| (6) |
_____
|
In an even parity checksum scheme: |
|
||
| (7) |
_____
|
The RS232-C protocol: |
|
||
| (8) |
_____
|
GPS satellites transmit: |
|
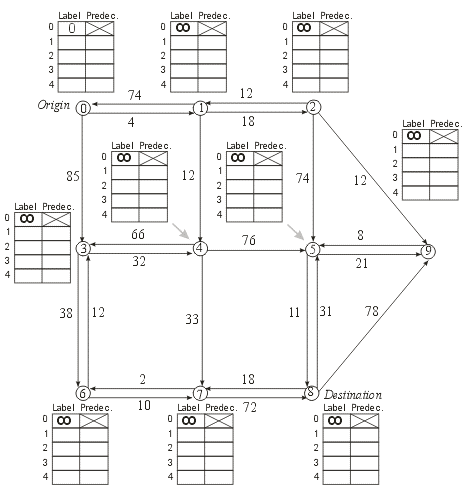
calculate the "shortest" path from vertex/node 0 to vertex/node 8 using Dijkstra's label setting algorithm. Show your work in the tables next to each vertex/node (i.e., each time you change the label associated with a vertex/node you must add a row to the associated table that contains the new label and the new predecessor).
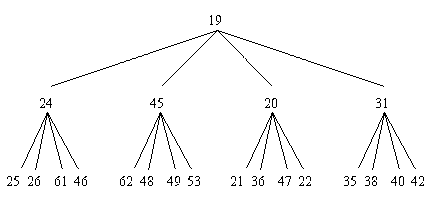
Node class:
public class Node
{
public int label;
public String id;
}
complete the following GroupedCollection
class:
import java.util.*;
/**
* A GroupedCollection is a collection of Node objects.
* Each node is kept in a "bucket" that corresponds to
* an intervale of labels.
*
* For example, if the maximum label is 100 and the
* number of buckets is 2, then the Node objects are
* kept in two buckets, one containing Node objects with
* labels in the interval [0, 50] and one containing Node
* objects with labels in the interval [51, 100].
* corresponding to its label.
*/
public class GroupedCollection
{
/**
* Explicit Value Constructor
*
* @param maxLabel The value of the largest possible label
* @param numBuckets The number of buckets
*/
public GroupedCollection(int maxLabel, int numBuckets)
{
}
/**
* Add a Node to this GroupedCollection (i.e., put
* it in the appropriate bucket)
*
* Note: This method assumes that the Node is not
* already in this GroupedCollection
*/
public void addNode(Node node)
{
}
/**
* Get the Node with the smallest label (and remove it
* from this GroupedCollection)
*
* @retun The appropriate Node
*/
public Node getNodeWithSmallestLabel()
{
}
/**
* Modify the label of a Node that is already
* in this GroupedCollection (and move the Node
* to the correct bucket)
*
* @param node The Node to modify
* @param newLabel The new label for this Node
*/
public void modifyNode(Node node, int newLabel)
{
}
}
| The metric generated by the Euclidean norm |
|
|
|
|
| The metric generated by the rectilinear norm |
|
|
|
|
| The metric generated by the supremum norm |
|
|
|
|
| The "Post Office" metric |
|
|
|
|
Using this, find the minimum distance between each of the following points and the line segment connecting the points (1,1) and (4,4).
16 ^ 16
|
|
|
|
|
(7 + 4) % 8
|
|
|
|
|
(211 + 32) % 256
|
|
|
|
|
1 ^ 2 ^ 3 ^ 4
|
|
|
|
|
JMUmble. In this system, arriving messages are
handled by a PostOffice object. Depending on how the
system is configured at runtime, one or more objects might need to
know when a message arrives. I have currently implemented several
such classes: Flasher (which makes a light near the
speedometer flash),
PopularityTimer (which starts a clock on your radio
that show the amount of time since the most recent message
arrived), and Mumbler (which uses speech generation
to read the name of the person that sent the message -- this is
where the system got its name). Use the observer pattern to
develop a class model of this system (in UML). You do not need to
include the attributes of each class, only the
operations/methods. Include comments that describe each
operation/method.

Point class discussed in lecture,
trace the execution of the following application (that was developed
as part of a system for partitioning spatial data):
public class Subdivide
{
public static Point i, j, one, startMax, startMin;
public static void main(String[] args)
{
double[] v;
// Create the unit vector i = (0,1)
v = new double[2];
v[0] = 1.0;
v[1] = 0.0;
i = new Point(v);
// Create the unit vector j = (1,0)
v[0] = 0.0;
v[1] = 1.0;
j = new Point(v);
// Create the vector one = (1,1);
one = i.plus(j);
// Create the vector lowerLeft = (0,0)
v[0] = 0.0;
v[1] = 0.0;
startMin = new Point(v);
// Create the vector upperRight = (4,4)
v[0] = 4.0;
v[1] = 4.0;
startMax = new Point(v);
// Quarter the rectangle formed by (0,0) and (4,4)
quarter(startMin, startMax);
}
public static void quarter(Point min, Point max)
{
Point delta, rho, tmin, tmax;
System.out.println("Min: "+min+" Max: "+max);
rho = max.minus(min);
delta = rho.times(0.5);
if (delta.gt(one))
{
// NW
tmin = min.plus(j.ctimes(delta));
tmax = tmin.plus(delta);
quarter(tmin, tmax);
// NE
tmin = min.plus(delta);
tmax = tmin.plus(delta);
quarter(tmin, tmax);
// SE
tmin = min.plus(i.ctimes(delta));
tmax = tmin.plus(delta);
quarter(tmin, tmax);
// SW
tmin = min;
tmax = tmin.plus(delta);
quarter(tmin, tmax);
}
}
}
\(y = 10 + x^{2}\)
\(y = 2 + x^{4}\)
You must find non-negative values of \(x\) and \(y\) that solve this system. Specifically, you must use the Golden Section algorithm to find the value of \(x\) that minimizes:
\([(10 + x^{2}) - (2 + x^{4})]^{2}\)
Show three iterations of the Golden Section algorithm starting with a lower bound of \(L = 0\) and an upper bound of \(R = 3\).
Copyright 2025