Sample Questions for Exam 2

Answer the questions from homeworks 4, 5, 6 and 7.
Answer the questions from chapters 3-4 in the textbook.

Choose the best answer to each of the following:

(1)	`_____`	A /27 CIDR network contains at most:
		16 hosts 32 hosts 64 hosts 128 hosts None of the above
(2)	`_____`	The mask `11111111.11111111.11111000.00000000` corresponds to a:
		A /11 CIDR network A /21 CIDR network A /24 CIDR network All of the above None of the above

Carefully define each of the following terms (as we have used them in this course):

Persistence (in the sense of HTTP)

Graph
Explain the difference between connection-oriented and connectionless transport layer protocols. Is this the same as the differene between stream-oriented and message-oriented protocols?
Compare and contrast UDP, TCP and SCTP.
When we discussed TCP we used a state diagram. When we discussed UDP we didn't. Why?
Explain why, in TCP, the client must acknowledge the SYNACK (also known as the ACKofSYN) sent by the server.
The following sequence diagram illustrates a particular example of sliding window flow control. Suppose that sequence numbers are 3 bits and that the initial window size is 7. Show both the transmitter's and receiver's window at every important time.
In the following timing diagram, how long is the propagation delay and how long is the transmission delay for the first frame?
When is stop-and-wait flow control particularly inefficient? Why?
Convert the IP address 198.58.104.19 to binary. How can you use the binary representation to determine that this is a class C address?
Consider a device with an address of 212.43.43.33 and a mask of 255.255.255.224.
1. What is the subnetwork for this device?
2. What is the corresponding CIDR address?
Explain why IP fragmentation tends to increase the overall amount of data that is transmitted.
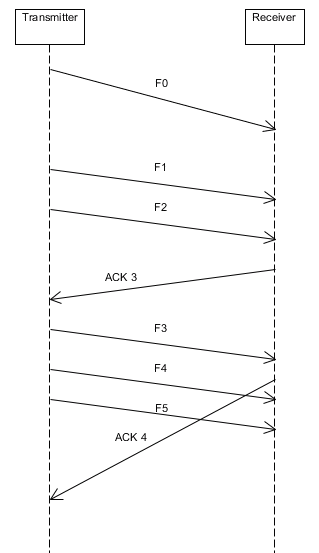
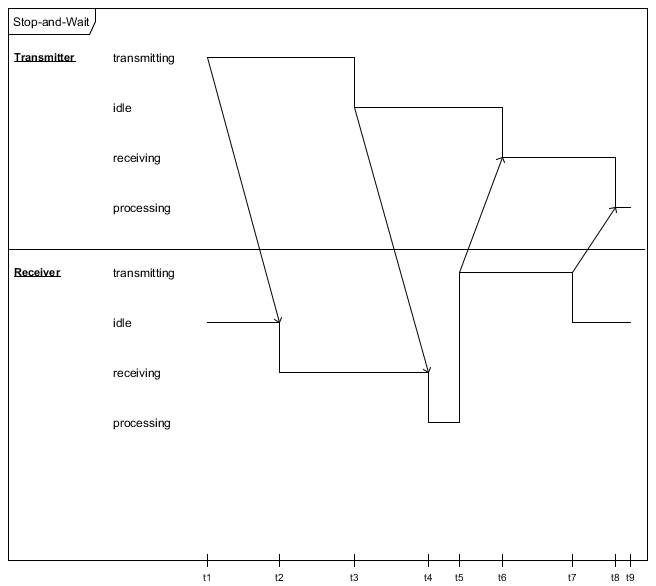
Given the following illustration of a directed graph (where the numbers next to an edge/link represent its "length"):
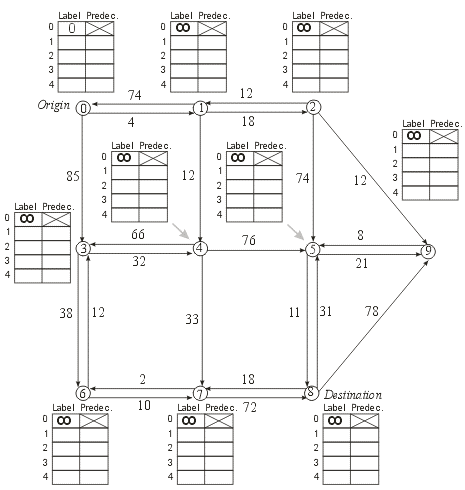
calculate the "shortest" path from vertex/node 0 to vertex/node 8 using the Dijkstra's label setting algorithm (as discussed in lecture). Show your work in the tables next to each vertex/node (i.e., each time you change the label associated with a vertex/node you must add a row to the associated table that contains the new label and the new predecessor).
Consider the following network in which all of the edges are bi-directional.

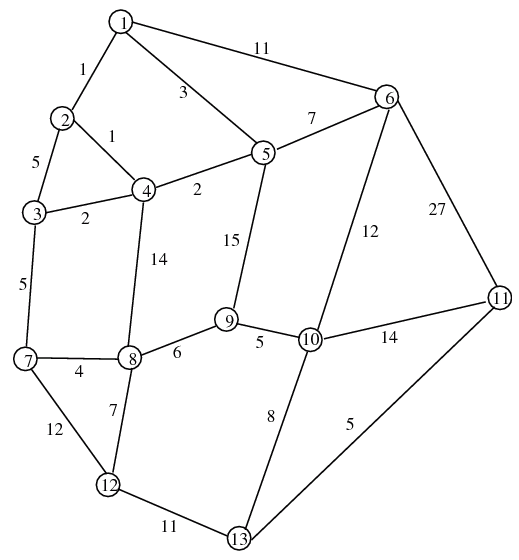
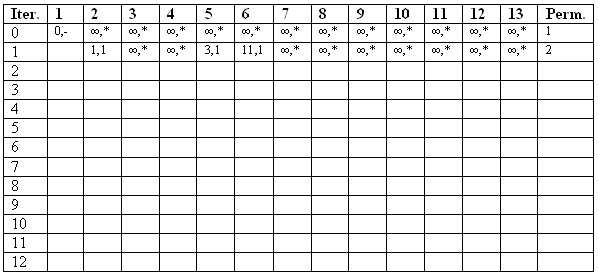
Show that the "shortest" path from vertex/node 1 to vertex/node 11 is 1-5-6-10-13-11 which has a "length" of 35. You must use Dijkstra's label setting algorithm (as discussed in lecture). Show all of your work in the table below (where iterations 0 and 1 have already been completed).
Imagine a system in which each message consists of two data bits and one parity bit. Suppose the probability that an individual bit is corrupted is given by \(p\), and that the probability that one bit is corrupted is independent of the probability that any other bit is corrupted.
Now, suppose that a message of 00 is transmitted with a (correct) parity bit of 0. What is the probability that the message is corrupted and that the error is not detected? (Hint: Carefully list all of the outcomes/events and assign probabilities to them.)