Sample Questions for the Final Exam

Answer the sample questions for exams 1, 2, and 3.
Answer the questions on exams 1, 2, and 3.
Carefully define/explain the following:

Hash Function

Binary Search Tree

3-Heap

Collision

Complete Graph

Indicate whether each of the following statements is true or false:

(1)	`_____`	Collisions improves the performance of a hashmap.
(2)	`_____`	Every node in a 3-heap has exactly three parents.
(3)	`_____`	The merge sort algorithm always outperforms the selection sort algorithm.

What is for the algorithm (we discussed in lecture) for inserting a node into a binary search tree? Use notation.
Discuss the advantages of chaining over probing (for collision resolution).
Using the following hash function:
```
int hash(int key)
{
    int result;

    result = key % 2;
    return result;
}
```
insert the following keys:
```
  5
  4
  2
  1
  3
  7
  8
  
```
into a chained hashmap. Show all of your work for each insertion.
Is the hash() function in the previous question:
1. Perfect? Why or why not?
2. A good hash function to use for a hashmap? Why or why not?

Complete the following function (that might be used, for example, in a mid-square hash function). Note: You should not concern yourself with leading zeroes.

  /**
   * Returns the middle digits of a number
   *
   * @param number     The number
   * @param numDigits  The number of digits in the return value
   *
   * @return           An int containing the middle digits 
   */
  int middleDigits(int number, int numDigits)
  {
    int middle;







    return middle;
  }

Write a function that would be appropriate for hashing a set of JMU course identifiers (e.g., CS139, CS239, ENG152).
Construct a binary tree that represents all of the possible outcome of tossing a coin three times.
Draw all possible binary search trees containing the four elements 1, 2, 3, 4.
Insert the numbers 49, 28, 66, 13, 35, 62, 80 (in order) into a binary search tree. Show all of your work. Discuss the properties of this BST.
Now insert the numbers 13, 28, 35, 49, 62, 66, 80 (in order) into a binary search tree. Show all of your work. Discuss the properties of this BST.
Write a function that finds the next-largest item in a subtree of a linked binary search tree. How would your answer change if the binary search tree is stored in a contiguous data structure?
Write a function that finds the height of a linked tree (with an arbitrary number of children).
Insert the numbers 9, 8, 4, 6, 2, 3 (in order) into a 2-heap using a linked data structure. Show all of your work.
Insert the numbers 9, 8, 4, 6, 2, 3, 1, 5, 7 (in order) into a 3-heap using a contiguous data structure. Show all of your work. (Make sure you describe the functions/algorithms you used to determine the indexes of parent and child nodes.)
Given the following illustration of a 4-heap:
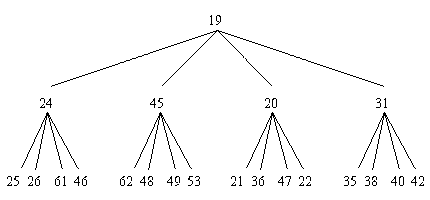
1. Change the 62 to a 49 and perform a "sift up".
2. Change the 46 to a 17 and perform a "sift up".
3. Remove the smallest element by swapping the "front" and "back" elements, removing the new "back" element, and performing a sift down.
4. Add a new element (with a value of 27) by making it the "back" element and performing a sift up.
Given the following illustration of a directed graph (where the numbers next to an edge/link represent its "length"):
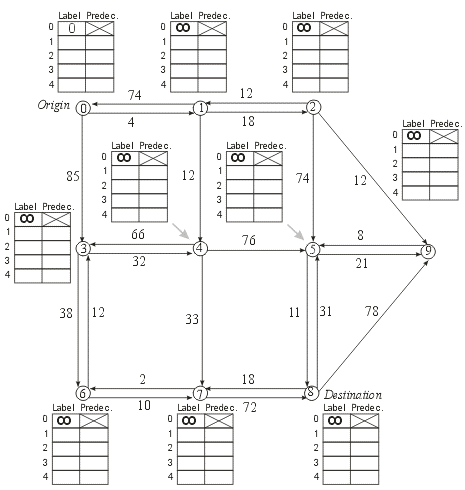
calculate the "shortest" path from vertex/node 0 to vertex/node 8 using the label setting algorithm discussed in lecture. Show your work in the tables next to each vertex/node (i.e., each time you change the label associated with a vertex/node you must add a row to the associated table that contains the new label and the new predecessor).